cannibol_90
Member level 5

Hi,
First of all, I hope everyone's fine!
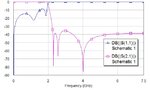
I am trying to implement elliptic filters using lumped elements and have been successful in designing one. The images below shows the circuit diagram and response of a 7th order elliptic Low-Pass filter.
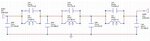
Now, one can easily find out the frequencies of the transmission zeros by evaluating the resonant frequencies of the parallel LC circuit.
Now, my questions are as follows;
1. How can one find out the frequencies corresponding to the S(1,1) dips from the lumped (LC) elements?
2. What does it mean when there is a frequency shift in the S(1,1) dips?
3. Also, what does it mean when one of the S(1,1) dips are missing? How can I bring it back to the original value/frequency, i.e. how can I adjust the L,C values to obtain the original plot?
Can someone help me? PLEASE!!!
First of all, I hope everyone's fine!
I am trying to implement elliptic filters using lumped elements and have been successful in designing one. The images below shows the circuit diagram and response of a 7th order elliptic Low-Pass filter.
Now, one can easily find out the frequencies of the transmission zeros by evaluating the resonant frequencies of the parallel LC circuit.
Now, my questions are as follows;
1. How can one find out the frequencies corresponding to the S(1,1) dips from the lumped (LC) elements?
2. What does it mean when there is a frequency shift in the S(1,1) dips?
3. Also, what does it mean when one of the S(1,1) dips are missing? How can I bring it back to the original value/frequency, i.e. how can I adjust the L,C values to obtain the original plot?
Can someone help me? PLEASE!!!
Attachments
Last edited: