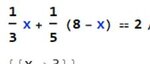Jayce
Newbie level 5

Problem : Tank A contains a mixture of 10 gallons water and 5 gallons pure alcohol. Tank B has 12 gallons water and 3 gallons alcohol. How many gallons should be taken from each tank and combined in order to obtain an 8 gallon solution containing 25% alcohol by volume?
From the book, 2 equations were derived based from the problem :
Equation 1 -> x + y = 8 & Equation 2 -> 0.3333x + 0.2y = 0.25(8)
My question : What is the formula used to get the 0.3333 and 0.2? Why or how is the formula designed like that? (Note : My question is not how to answer the problem.)
My thoughts / analysis : To get 0.33333, the fraction must be 1/3. So from the first tank, we have 10 gallons of water and 5 gallons of pure alcohol.
So, 5 / (10 + 5) = 5 / 15 = 1/3 = 0.33333. If we used that on 2nd tank, we will get the 0.2
So, If we are to put it into words :Mixture of gal. of water and pure alcohol = x gallons of alcohol / (x gallons of alcohol + x gallons of water).
The question is why or how is that the formula for mixing the gallons of alcohol and water? In my mind it should be just an addition between the 2, water + alcohol = mixture.
Sorry If the question is silly but thanks in advance for those who can explain it clear. God bless.
From the book, 2 equations were derived based from the problem :
Equation 1 -> x + y = 8 & Equation 2 -> 0.3333x + 0.2y = 0.25(8)
My question : What is the formula used to get the 0.3333 and 0.2? Why or how is the formula designed like that? (Note : My question is not how to answer the problem.)
My thoughts / analysis : To get 0.33333, the fraction must be 1/3. So from the first tank, we have 10 gallons of water and 5 gallons of pure alcohol.
So, 5 / (10 + 5) = 5 / 15 = 1/3 = 0.33333. If we used that on 2nd tank, we will get the 0.2
So, If we are to put it into words :Mixture of gal. of water and pure alcohol = x gallons of alcohol / (x gallons of alcohol + x gallons of water).
The question is why or how is that the formula for mixing the gallons of alcohol and water? In my mind it should be just an addition between the 2, water + alcohol = mixture.
Sorry If the question is silly but thanks in advance for those who can explain it clear. God bless.