yefj
Advanced Member level 4

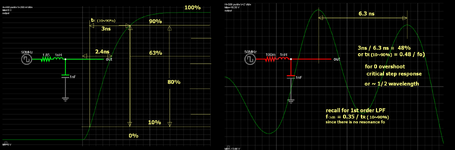
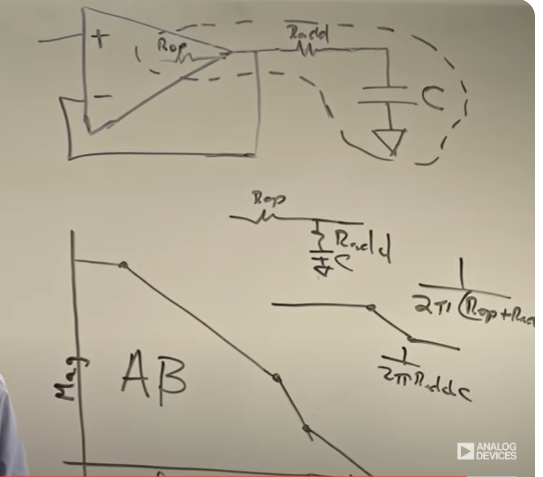
Hello , on the third minute of the manual shown in the link at minute 3 he says that when we add a resistor our added pole is 1/(Rop+Radd)C
Then he says that when the impedance of the capacitor in the same order ar the added resistor then we have a ZERO effect and the slope gets less steep.
How does a pole can turn to zero?
What is the math behind it?
Thanks.
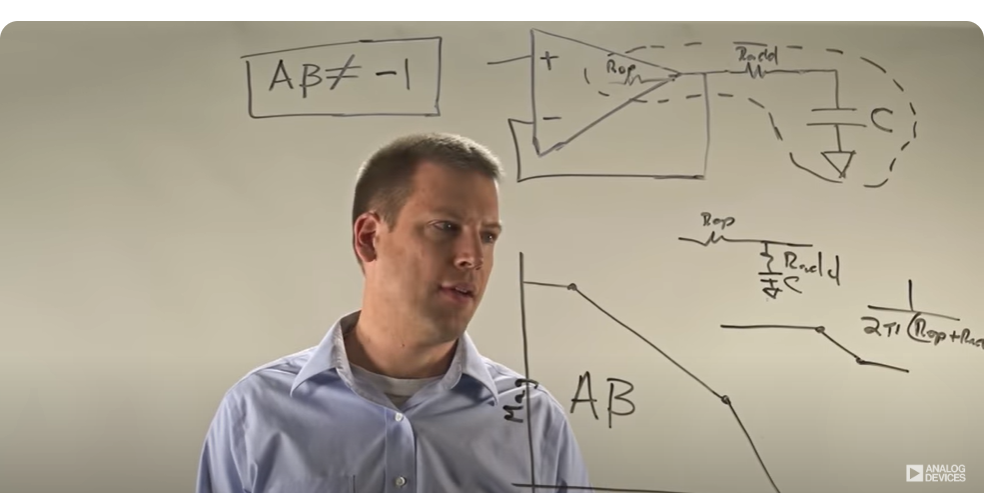
Then he says that when the impedance of the capacitor in the same order ar the added resistor then we have a ZERO effect and the slope gets less steep.
How does a pole can turn to zero?
What is the math behind it?
Thanks.