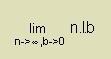subharpe
Full Member level 4

- Joined
- Jan 9, 2008
- Messages
- 207
- Helped
- 25
- Reputation
- 50
- Reaction score
- 2
- Trophy points
- 1,298
- Location
- Bangalore,India
- Activity points
- 2,657
Can someone tell me which function is integrable (analytically, not numerically) and which function is not and how to trace from the expression of the function?