dressler6
Newbie level 6

This is the case of a 3 stage amp with negative feedback.
The output is a source follower, so amplification is done twice.
If you look at the method of finding the loop gain using lstb in hspice, the phase margin is 90'.
However, there is gain peaking at frequencies after the unit gain frequency, and the gain margin is -20dB.
The following are my questions.
1. When this circuit is enabled, oscillation occurs. It is clearly stable in the lstb simulation of the steasy state. Please explain how it can be verified with a simulation other than '.tran' (e.g. AC simulation or lstb simulation or .pz simulation).
2. The control system considered that the stability of the transient section should be checked with the characteristic equation of the closed loop transfer function.
Does that mean it should be viewed as a root locus?
3. If number 2 is correct, sweep the variable k at the root locus, how should it be applied to the above-mentioned regulator?
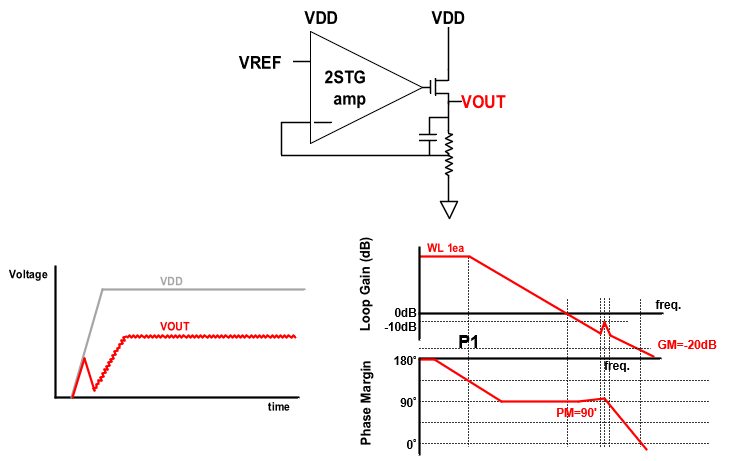
The output is a source follower, so amplification is done twice.
If you look at the method of finding the loop gain using lstb in hspice, the phase margin is 90'.
However, there is gain peaking at frequencies after the unit gain frequency, and the gain margin is -20dB.
The following are my questions.
1. When this circuit is enabled, oscillation occurs. It is clearly stable in the lstb simulation of the steasy state. Please explain how it can be verified with a simulation other than '.tran' (e.g. AC simulation or lstb simulation or .pz simulation).
2. The control system considered that the stability of the transient section should be checked with the characteristic equation of the closed loop transfer function.
Does that mean it should be viewed as a root locus?
3. If number 2 is correct, sweep the variable k at the root locus, how should it be applied to the above-mentioned regulator?
