A question for implementing Cryptographic algorithms

[Herc11]

Hello,
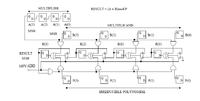
I have a question to make concerning the basics of cryptography. When algorithms are implemented in Galois Field (e.g. 2^128) what is easier to use? Polynomial or standard integer modular arithmetic ? I mean at the way that data have to be expressed. Is there a significant difference between and If yes when it is preferable to use the one way or the other?

 

[elockpicker]

Hi,
I've implemented a few cryptographic algorithms in Verilog and now that I look back I think the easiest way to handle the data is the format suggested by the algorithm reference.

Usually you don't even have to have an in-depth familiarity with the mathematics behind the algorithm,just look at it like a vector (or matrix) of data.

Cryptographic algorithms usually contain a number of finite field multiplications which often have a predetermined operand, like :
A x 0x2C = (A times 0x2C)
or
B x 0xF3 = (B times 0xF3)
In cases like this you'll have to convert the multiplication to a simple logic circuit (if not provided by the algorithm reference) and use it your designs.

At the end, I think if you use another format for processing the data then you'll have to re-do some math calculations and that might result into errors.

Hope I helped.
Regards

 

[Herc11]

Thank you for your answer elockpicer.

The problem is that the algorithm that I have to implement is described over a Real field and so, I have to make the transformation of the implementation from Real to Galois field. Thus, I might be obliged to be mixed with mathematics and decide if I must use Polynomial or standard integer modular arithmetic. (This I meant when I was writing about the way that data have to be expressed.)
In the last days I am starting to thinking that polynomial arithmetic is the only solution when working over finite fields but I am not sure yet...

 

[elockpicker]

In my experience cryptographic algorithm have a residual nature, so it's very likely that you can convert the Real field algorithm to a Finite field one.
One important note is : working in Real field requires Real multipliers which consume a lot of chip area and also drastically lower the maximum applicable clock.
On the other hand Finite field multipliers are both tiny and very fast.
I don't know your designs goals (area, power or speed), but in any of the scenarios you probably wanna avoid Real (integer indeed) multipliers.

 

[Herc11]

Yes, I will avoid Real multiplications and in general calculations over Real numbers. But what is better to use? Polynomial arithmetic (irreducible polynomial etc) or calculations with integers i.e. data will have to be represented as polynomials or as integers?

 

[elockpicker]

In my opinion, finite field arithmetic is more compact than integer computations.

 

[Herc11]

I have another question concerning the implementation of a multiplier over a finite field. For example, I want to create a multiplier over GF(2^4). This means that I have to use registers which will store the two multiplicands, the result and the irreducible polynomial. I saw some implementations and algorithms and 4 bits registers are used for multiplicands and for the storage of the irreducible polynomial.
My question is that since irreducible polynomial over GF(2^4) has 5 coefficients namely x^4+x+1 i.e. its representation in polynomial basis is 10011, (5bits) how can it “fit” in a 4 bit register?
Thanks.

 

[elockpicker]

Hi,
Implementing finite field multiplications, is all about resource and performance optimization.
In many different applications, one multiplicand is always a constant number (i.e a constant member of the specified finite field) so the general form of that
Anyway, no one can fit five bits in four. If that's the case, there must be a constant bit in the 5-bit word. For example one of the bits can be always '0' or '1'.

 

[Herc11]

All of the bits I think that they are constant because the irreducible polynomial does not change. So you are saying that some bits(one)are omitted ??

 

[elockpicker]

probably,
if the irreducible polynomial is always constant, then there's no use keeping it in a register (in fact the synthesis tool converts the constant number into hardwired logic).
If there is a register for keeping the irreducible polynomial, then it must be changed or update sometimes (maybe once).
we have to take a closer look at the implementation...

 

[Herc11]

So, there is an example of a 4 bit multiplier provided by a pdf of Xilinx(image1) and the algorithm (image 2)that is used . The irreducible polynomial is the 10011 x^4+x+1. I can not understand how the irreducible polynomial is stored into the P(..) register. And when I ll implement the code I will have to use a 4 bi register or a 5 bit? I ll hope that i ve uploaded the figures right...

 

[costello_env]

Hii Everyone!
I'm new to Neural Networks and with the help of certain tutorials available online have managed to understand the concept of Neural networks and various models available. Currently i'm working on Hopfield Neural Networks, which are binary networks. I want the network to be trained with certain patterns(text input) initially and then recall them when given as input. The problem is i'm unable to come up with the network in matlab using the function "newhop".
Can someone please help me how to go about with it in matlab or provide me any source for materials or code if available on the same. Its really urgent.