[SOLVED] 3d coordinate rotation

[pisoiu]

Hi all,

Maybe a lot of years ago my math was in better shape, but now it is gone, so I need some help.
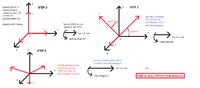
I need to rotate a coordinate system. I have an accelerometer which gives me accelerations on all 3 axes, X, Y, Z as 8 bit signed values. The accelerometer is mounted on a mobile platform but the accelerometer axis does not match the platform axis, so I need to rotate the X,Y,Z of the accelerometer into X', Y' and Z' of the platform, where let's say X' is the forward direction of the platform, Y' is side and Z' point towards earth.
From what I have been able to find over the net, the X', Y' and Z' can be calculated with the followinng formulas:

X'=X*cos(\[\alpha\]_x)+Y*cos(\[\alpha\]_y)+Z*cos(\[\alpha\]_z)
Y'=X*cos(\[\beta\]_x)+Y*cos(\[\beta\]_y)+Z*cos(\[\beta\]_z)
Z'=X*cos(\[\gamma\]_x)+Y*cos(\[\gamma\]_y)+Z*cos(\[\gamma\]_z)

where \[\alpha\]_x,y,z is the angle between X' platform axis and each accelerometer axis (X,Y,Z), \[\beta\]_x,y,z is the angle between Y' platform axis and each accelerometer axis and similar for \[\gamma\]
between all these angles, there is a relation
\[\alpha\]_x+\[\alpha\]_y+\[\alpha\]_z=\[\beta\]_x+\[\beta\]_y+\[\beta\]_z=\[\gamma\]_x+\[\gamma\]_y+\[\gamma\]_z=180^o
also
\[\alpha\]_x+\[\beta\]_x+\[\gamma\]_x=\[\alpha\]_y+\[\beta\]_y+\[\gamma\]_y=\[\alpha\]_z+\[\beta\]_z+\[\gamma\]_z=180^o

In order to determine the coefficients (cos\[\alpha\],\[\beta\],\[\gamma\]..) two calibrations are required, first with 0 acceleration on X' and Y', leaving only Z'=1G (gravitational acceleration). This will determine the direction of Z' axis. A second calibration is required to determine the forward direction of the platform, X'. Then, knowing X' and Z', Y' should be possible to determine. The difference between these two calibration procedures, would be that for Z', the amount is known, it is 1G, but for X', the value will not be known.
The equations for calibration for non-moving platform should be:

X' : X1*cos(\[\alpha\]_x)+Y1*cos(\[\alpha\]_y)+Z1*cos(\[\alpha\]_z)=0
Y' : X1*cos(\[\beta\]_x)+Y1*cos(\[\beta\]_y)+Z1*cos(\[\beta\]_z)=0
Z' : X1*cos(\[\gamma\]_x)+Y1*cos(\[\gamma\]_y)+Z1*cos(\[\gamma\]_z)=1G
where X1,Y1,Z1 are readouts from accelerometer when platform is not moving

The equation for calibration for forward accelerating platform should be

X' : X2*cos(\[\alpha\]_x)+Y2*cos(\[\alpha\]_y)+Z2*cos(\[\alpha\]_z)=unknown constant
Y' : X2*cos(\[\beta\]_x)+Y2*cos(\[\beta\]_y)+Z2*cos(\[\beta\]_z)=0
Z' : X2*cos(\[\gamma\]_x)+Y2*cos(\[\gamma\]_y)+Z2*cos(\[\gamma\]_z)=1G
where X2,Y2,Z2 are readouts from accelerometer when platform is pushed forward

What I do not know is how to extract the coefficients (cos\[\alpha\],\[\beta\],\[\gamma\]) from calibration equations in order to use them into general X', Y' and Z' equations.
All the implementation will be done in 8bit assembly language, so the operations must be broken into what the CPU is able to do (8 bit add, subtraction, division and multiplication). The code to implement the general equations is already done, but the part with coefficients extractions is still a mistery.

Thanks.

Best regards,

 

[CataM]

Your equations are difficult to solve showed that way. In Robotics there are Rotational Matrices that give rotational movement a bit easier. Search Roll-Pitch-Yaw or Euler 3-2-1.

3 angles: alpha,beta, gamma are sufficient to define rotation. There is no need of 9 angles.

 

[andre_luis]

If the calibration is performed statically just by using the gravity as input, the "rotation" notion could be applied, therefore simplifying the analysis, once the vectorial sum of all axis should result in G; However, I think that the addition of an accelerated movement in the system should be considered generically as a "transforming" operation.

 

[pisoiu]

I saw some papers regarding rotational matrices but I did not understood it very well, or how to break complicated equations into more simple operations which can be transposed in assembly language. Connecting calibration equations with rotation equations is my real problem. I will study it again but my hopes are dim..

3 angles: alpha,beta, gamma are sufficient to define rotation. There is no need of 9 angles.

Either I do not understand something too well (which is very probabaly) or three angles are not enough.
Let's start with above notations, XYZ being accelerometer coordinates and X'Y'Z' being platform coordinates.
Assume alpha is the angle between X' and X, beta is between X' and Y and gamma is between X' and Z. Imagine you rotate the platform coordinates spinning X' axis. The plane defined by Y' and Z' which is perpendicular on X' will rotate around X' (changing Y' and Z' axis position) but the angles between X' and X,Y respectively Z will remain the same.

If the calibration is performed statically just by using the gravity as input, the "rotation" notion could be applied, therefore simplifying the analysis, once the vectorial sum of all axis should result in G;

Yes, this will give Z' axis direction, but how would I know which is front/back (X') or left/right (Y')?

Thanks.

 

[andre_luis]

I would recomend you take a top-down approach, and instead of getting equations on the web with the projection of the angle at each axis, at this stage you could simplify the analysis just making a general mactricial equation for the whole operation, such as ( I'm not sure if it is correct ):

• \[\vec{ X'}\] = ( \[\vec{ X}\] x \[\vec{ \phi}\] ) + \[\vec{A}\] , where A represents the acceleration vector.

This way, you could make some numerical experiments on MATLAB/SCILAB in order to validate the model for known measured values. For instance, you could put the object in 3 the orthogonal x,y,z directions, resulting in A=[g_x,0,0], [0,g_y,0] and [0,0,g_z] respectively.

 

[CataM]

Let's start with above notations, XYZ being accelerometer coordinates and X'Y'Z' being platform coordinates.
Assume alpha is the angle between X' and X, beta is between X' and Y and gamma is between X' and Z. Imagine you rotate the platform coordinates spinning X' axis. The plane defined by Y' and Z' which is perpendicular on X' will rotate around X' (changing Y' and Z' axis position) but the angles between X' and X,Y respectively Z will remain the same.

There are 2 methods.

FIRST: Rotate system around stationary system's axis (called Roll Pitch Yaw)
SECOND: Rotate system around rotational system's axis (called Euler 3-2-1)

This is an illustration of Roll Pitch Yaw to see if this is what you say...



Roll-Pitch-Yaw method is used in aerospace domain to represent rotation. If planes can handle with 3 angles, your system too, so, I still maintain that 3 angles are sufficient.

---

I wrongly said that there are 2 methods, obviously there are more, but those are common. Those methods are just a way to represent rotation.

- - - Updated - - -

I know what are you meaning with alphaX, alphaY etc. It is the normal way everyone would do and the intuitive way.

That is not necessary. Knowing rotation angle around each axis, you are able to define some rotational matrixes which finally define a single matrix 3x3 called Rotational Matrix which gives you the rotation of system B with respect of system A. Thouse angles you are saying are included in that matrix in some expressions (cosines and sines) with the 3 angles, in other words, in your 3x3 Matrix you will only have expressions depending on 3 angles only.

But how do you get that Rotational Matrix and is not needed those 9 angles?
Answer: Multiplying each matrix after each rotation, meaning , those angles alphaX,alphaY etc, are represented in those multiplications.

Conclusion: Choose a method to represent rotation (Euler,Roll etc) and then find that Rotational Matrix 3x3 (which is obtained by multiplications of other matrixes).

In addition to that Rotational Matrix, if you want to express spatial localization of an object in 3D (spatial localization=orientation + position), that is represented with a 4x4 Matrix called Transformation Matrix which is formed by the Rotational Matrix 3x3 (mentioned above) + position vector.

 

[CataM]

Your equations on post 1 are correct, which is how rotational matrix is defined.



"ix" in that picture and so on are unity vectors along x axis and so on. Scalar product of 2 unit vectors is just the cosine of the angle they form.

But after you spin it around 1 axis, the matrix will simplify remaining zeros.

If you make spin after spin, then you have a composition of rotations, which leads to multiplying matrixes (3 spins = 3 matrixes that have to be multiplied).

Example:
To the system OUVW (accelerometer) is applied rotations as follows:
First: alpha degrees around OX.
Second: phi degrees around OY.
Third: theta degrees around OZ.

The global rotation is expressed as follows:



Hope now is a bit clearer.

 

[pisoiu]

Thank you all for answers, it is a bit clearer now.