Input reflection coefficient

[andrew_que]

Hello.
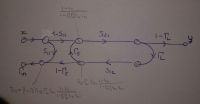
To get the reflection coefficient at the input (port 1) of a two ports device knowing its scattering matrix and the load at port 2 one can use the formula \[\Gamma_{in} = s_{11} + \frac{s_{12}s_{21}\Gamma_L}{1-s_{22}\Gamma_L}\], but I don't quite get it. I can see that when a wave enters the device, part of it is reflected back (s11). The remaining wave (1-s11) is free to cross the device and a portion s21 of it reaches the end (the other port). Then, a portion GL (gamma L) of this is reflected back and again the portion s12 reaches back port 1. So far we have \[\Gamma_{in} = s-{11} + c(1-s_{11})s_{12}s_{21}\Gamma_L\], where c represents how much of the second part can actually exit port 1 due to further reflections to sum it up properly to s11, but i don't know how to evaluate that.. The formula takes into account also s22, but i don't see how can port 2 affect this since we're at port1..
I have the feeling my whole line of reasoning is flawed, I'd be grateful to anyone able to correct me!
Thank you in advance

 

[BigBoss]

The key player is S12 here.If you make it zero, Gamma_in will be equal to S11.
All those equations come from "Mason's Flow" technique.

 

[andrew_que]

I already thought about that but never tried because I'm missing something here.
Here I made some hand calculations.

If everything is fine and I use the right value for \[\Gamma_S\] (which I don't know) I should be able to retrieve the previously mentioned formula. So I tried to solve for \[\Gamma_S\] by equating the bottom left equation with the formula but I get a long strange expression that doesn't really mean anything to me...

 

[BigBoss]

I already thought about that but never tried because I'm missing something here.
Here I made some hand calculations.

If everything is fine and I use the right value for

(which I don't know) I should be able to retrieve the previously mentioned formula. So I tried to solve for

by equating the bottom left equation with the formula but I get a long strange expression that doesn't really mean anything to me...

Gamma_S=0 in normal conditions.
Gamma_S=Source Reflection Coefficient

 

[andrew_que]

Turns out there were still a couple of problems on top of that that made the flowchart wrong:
1 - No need to add the (1-s11) branch: it is implicit in the definition of s21
2 - The node I marked C is actually a2 whereas B is b2, so a branch s22 connecting the two nodes is missing
Thank you very much!