julian403
Full Member level 5

Hello, I have to analize the boost dc-dc converter.
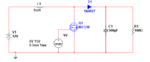
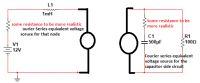
This has two operation mode. One when the transistor is on and second when transistor is off.
When transistor is on, in the first mode. The ecuation is:
\[ V = {r}_{on} {i}_{1}(t) + L \frac{d {i}_{1}(t)}{dt}\] where \[{r}_{on} = 0.01 \Omega \]
And the second mode it's
\[ V + L {{i}_{1}}^{0-} = L \frac{d {i}_{2}(t)}{dt} + R {i}_{2}(t) + \frac{1}{C} \int {i}_{2}(t) dt + \frac{{{i}_{2}}^{0-}}{C}\]
The problem here is the initial condition \[{i}_{1}^{0-}\] and \[{i}_{2}^{0-}\]of the diferential ecuation which it's growing until it reaches to the permanet condition.
How many step I must consider? because there is two times constants. One for the first mode's circuit and other for the second mode's circuits. For the firts mode circuit the time constant is L/r_on and for the second mode's circuit is ≈ Π/(RC) that's because it's a second order's system.
I need to know that for example if there is the need to know if the circuit is a continouos current or discontinouos current.

This has two operation mode. One when the transistor is on and second when transistor is off.
When transistor is on, in the first mode. The ecuation is:
\[ V = {r}_{on} {i}_{1}(t) + L \frac{d {i}_{1}(t)}{dt}\] where \[{r}_{on} = 0.01 \Omega \]
And the second mode it's
\[ V + L {{i}_{1}}^{0-} = L \frac{d {i}_{2}(t)}{dt} + R {i}_{2}(t) + \frac{1}{C} \int {i}_{2}(t) dt + \frac{{{i}_{2}}^{0-}}{C}\]
The problem here is the initial condition \[{i}_{1}^{0-}\] and \[{i}_{2}^{0-}\]of the diferential ecuation which it's growing until it reaches to the permanet condition.
How many step I must consider? because there is two times constants. One for the first mode's circuit and other for the second mode's circuits. For the firts mode circuit the time constant is L/r_on and for the second mode's circuit is ≈ Π/(RC) that's because it's a second order's system.
I need to know that for example if there is the need to know if the circuit is a continouos current or discontinouos current.