amirhossein20n
Junior Member level 1

hello everybody
can anybody help me
i want to solve this nonlinear equation in form of closed solution , i mean not by usual nonlinears solution such newton method and other estimation methods ... . the form of solution that by changing the defind parameter , the solution can be observed.
sincerely
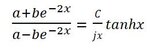
- - - Updated - - -
reminding that a,b & c are arbitrary numbers but cant be eliminated or combined. thanks
can anybody help me
i want to solve this nonlinear equation in form of closed solution , i mean not by usual nonlinears solution such newton method and other estimation methods ... . the form of solution that by changing the defind parameter , the solution can be observed.
sincerely
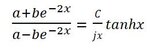
- - - Updated - - -
reminding that a,b & c are arbitrary numbers but cant be eliminated or combined. thanks
Last edited:



