mordak
Member level 5

Hey guys,
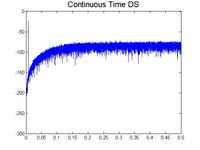
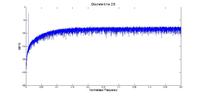
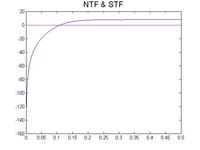
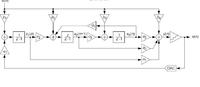
I have simulate both discrete and continuous time delta sigma ADCs and came across a weird problem. In continuous time delta sigma, unlike discrete one, stability of the converter depends on the frequency of the input signal. Say there is a low-pass, continuous time, 500kHz delta sigma ADC, (Fs = 32MHz), I expected if I apply 4MHz input signal, I will not be able to reconstruct the signal, since input is far away from the filter bandwidth. But still ADC should work properly without any saturation. However, what I observed was having all integrators in ADC being saturated. I was wondering if I missed anything, or it's a normal phenomenon.
I have simulate both discrete and continuous time delta sigma ADCs and came across a weird problem. In continuous time delta sigma, unlike discrete one, stability of the converter depends on the frequency of the input signal. Say there is a low-pass, continuous time, 500kHz delta sigma ADC, (Fs = 32MHz), I expected if I apply 4MHz input signal, I will not be able to reconstruct the signal, since input is far away from the filter bandwidth. But still ADC should work properly without any saturation. However, what I observed was having all integrators in ADC being saturated. I was wondering if I missed anything, or it's a normal phenomenon.