hyleeinhit
Member level 3

Hi, folks,
For a current integrator, say a amplifier with a 5pf feedback capacitor, what the requirement of the amplifier phase margin (PM)?
I know for a buffer, the amplifier phase margin would be at least larger than 45 degree. What is the difference between these two cases? Thanks.
The following is my understanding on PM:
OTA open loop PM requirement is calculated with loop gain. For a closed-loop system with a closed loop gain larger than 1, OTA open loop PM requirement is lower, i.e., can be lower than 45 degree. A buffer (closed gain is equal to 1) has the worst situation and requires largest OTA open loop PM. To make PM definition clear, I attached my open loop an analysis setup and result here.
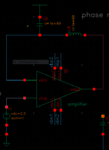

From the result you can see, the OTA open loop gain is 76.71dB, UBW is 7.9MHz and open loop PM is (180-126.4)=53.6 degree.
I do not know how to calculate a current integrator loop gain since the input can be any current.
For a current integrator, say a amplifier with a 5pf feedback capacitor, what the requirement of the amplifier phase margin (PM)?
I know for a buffer, the amplifier phase margin would be at least larger than 45 degree. What is the difference between these two cases? Thanks.
The following is my understanding on PM:
OTA open loop PM requirement is calculated with loop gain. For a closed-loop system with a closed loop gain larger than 1, OTA open loop PM requirement is lower, i.e., can be lower than 45 degree. A buffer (closed gain is equal to 1) has the worst situation and requires largest OTA open loop PM. To make PM definition clear, I attached my open loop an analysis setup and result here.


From the result you can see, the OTA open loop gain is 76.71dB, UBW is 7.9MHz and open loop PM is (180-126.4)=53.6 degree.
I do not know how to calculate a current integrator loop gain since the input can be any current.
Last edited:




