Concept of Negative Feedback question

[okami11408]

I'm new here, I'm currently learning about basic negative feedback network and have a few question about concept of the negative feedback.

This is what I understand about negative feedback, I know that the gain of negative feedback is independent to Av because close loop gain(Af) is equal to A/(1+Aβ)

and A is very big, so Af=1/β.

----------------------------------------

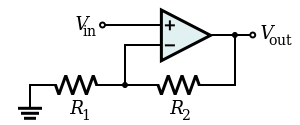
My question is according to the circuit below, why we call (Vi-Vfb) as an error signal(Vε) I mean why it's an error, and why we have to amplify that error?

And after we amplify that error we get Vout(amplified error signal) this is what confused me, we always use Vout to power something,

but it's and error signal that power something????8-O

More confusing on β circuit, I know that β is very small, why it's very small?, we amplify that error and now we want it to be small again??:shock: and that small error(Vfb) become the part of Vi??

Vi now contains 2 error signals?????

I really don't understand the whole concept of it, please help.

Sorry for my English.

Here's the image

**broken link removed**

**broken link removed**

 

[FvM]

Error signal is a basic term in control theory for the difference between setpoint and process value https://en.wikipedia.org/wiki/PID_controller

 

[LvW]

Quotation: This is what I understand about negative feedback, I know that the gain of negative feedback is independent to Av because close loop gain(Af) is equal to A/(1+Aβ)
and A is very big, so Af=1/β.

The forward open-loop gain is "very big" only in case of an opamp. In other applications (control systems) it can assume all values from small to large.


Quotation: My question is according to the circuit below, why we call (Vi-Vfb) as an error signal(Vε) I mean why it's an error, and why we have to amplify that error?

As mentioned by FvM - this term originates from control theory, which also is based on negative feedback concept. It is the task of a control loop to have an output signal that follows a certain reference signal.
For this purpose, a part of the ouput is fed back to a unit that compares the reference and the feedback signal.
If both signals are not yet equal (within some uncertainty limits) the difference between both - the error signal - causes a change of the output until this goal is achieved.
In opamp applications the output shall equal the input multiplied by a factor (gain). Therefore a part of the output is fed back to compare it with the applied signal. This is the reason the input difference (which approaches zero for very large A) sometimes is called "error signal". But it is in no case something like an "error". It is just the small input differential signal driving the opamp.
The term "error signal" is used primarily by authors who comes from the control systems side. Most electronic engineers rather speak about the opamp input difference voltage.

Quotataion: More confusing on β circuit, I know that β is very small, why it's very small?, we amplify that error and now we want it to be small again?? and that small error(Vfb) become the part of Vi??


No, the feedback signal beta is not always "very small". For unity gain amplifiers (buffers) it is unity (100% feedback) .

I hope it is clear now.

Regards
LvW

 

[okami11408]

Thank you for the reply but I still confuse about the way input see different and amplify it.

This circuit for example.

Let's say if VR1=1/2Vout

When the inputs see a difference, say 1V and 0V, the amp massive gain (say 1000) amplifies the difference(1V).

Now Vout is 1000V, half of this was fed back to the inverting terminal. The inputs will be 1V and 500V, Vi=500-1=499V

Again Vout is 499x1000=499000V. The inputs will be 1V and 499000V.

Why Vout is getting bigger??

 

[LvW]

Okami,

I suppose you need first to become familiar with the principle of negative feedback. In this context, some further remarks:

* At first, be exact in writing equations and formulas. Otherwise, nobody can understand you. What is "VR1"? A product of V and r1? What means 1/2Vout ? One divided by 2*Vout? Use brackets to make it clear.
* Secondly, you have to discriminate between the transient behaviour (switch-on effects starting at t=0) and the steady-state after feedback has produced an equilibrium. All the formulas (gain, ) can be applied for this state only. It is the result of feedback that a voltage across R1 is produced (driven by the output voltage) that is nearly equal to Vin (in the above circuit).
* Therefore, as soon as you have Vin=1V the rising output causes a voltage across R1 which is only slightly below 1V (for example: 0.99999..volts) leading to a finite ouput of approx. Vin*(1+R2/R1).
* Exact value: Vout=Vin*[A/(1+beta*A)]=Vin*[1/(1/A + beta] with beta=R1/(R1+R2).

 

[crutschow]

Thank you for the reply but I still confuse about the way input see different and amplify it.

This circuit for example.

Let's say if VR1=1/2Vout

When the inputs see a difference, say 1V and 0V, the amp massive gain (say 1000) amplifies the difference(1V).

Now Vout is 1000V, half of this was fed back to the inverting terminal. The inputs will be 1V and 500V, Vi=500-1=499V

Again Vout is 499x1000=499000V. The inputs will be 1V and 499000V.

Why Vout is getting bigger??

The voltage output never gets that high. Look at it this way. You apply 1V at the input and the output voltage starts to rise (it has a finite rise time due to the op amp bandwidth). This voltage is reduced by the voltage divider R1 and R2. When the voltage at the junction of R1 and R2 equals 1V, the voltage at the op amp plus and minus terminals are equal and the output voltage stops rising and stays at this level. This occurs when Vin = Vout x R1/(R1+R2) which gives a gain of Vout/Vin = (R1+R2)/R1 (assuming very high op amp open loop gain).

 

[LvW]

When the voltage at the junction of R1 and R2 equals 1V,

Just a small correction (for a better understanding):
I would suggest to say: When the voltage at the junction of R1 and R2 comes very close to 1 V ..... (because it never will reach 1 Volt).

 

[FvM]

In addition:

Now Vout is 1000V, half of this was fed back to the inverting terminal. The inputs will be 1V and 500V, Vi=500-1=499V
Again Vout is 499x1000=499000V. The inputs will be 1V and 499000V.

If the output voltage would be 1000V (it actually can't for a real OP, as mentioned) then the input voltage would be -499V. You mixed up the gain sign, turning the negative into positive feedback.

 

[crutschow]

In addition:

If the output voltage would be 1000V (it actually can't for a real OP, as mentioned) then the input voltage would be -499V. You mixed up the gain sign, turning the negative into positive feedback.

Not for the circuit shown, which is a non-inverting amp. Both input and output have the same polarity.

 

[FvM]

Not for the circuit shown, which is a non-inverting amp. Both input and output have the same polarity.

You probably didn't look sharp. Vin is the differential OP input voltage, the large 500V term is the feedback generated part. It's surely opposite to Vout in a negative feedback circuit.

 

[D.A.(Tony)Stewart]

THe R2/R1 ratio always defines the inverting gain. Because the Op Amp has such a high DC gain usually 1million (1e6).
The OA compares the differential inputs +,- and adjusts the output until the input difference is zero.

If the (+) goes up the output goes up until the feedback voltage at (-) matches the input. Knowing that the OA Input current is tiny and thus resistance is much higher than R2//R1, we can neglect for now if say<10MΩ. So the OA will rise until the Vin- matches Vin+ and then reach an equilibrium where the voltage gain matches the R2/R1 ratio since they virtually share a common current from output to inverting input R1 to Gnd (0V) .


The Vout always has the same polarity as the Vin+ and would be 1e6 voltage gain if there was no negative feedback. Due to this negative feedback ratio R2/R1 the OA gain is reduced so that the inputs at Vin+=Vin- are equal.. i.e. zero input offset.

So imagine if the R2/R1 ratio was 1000 the output would amplify Vin+ x (1000 + 1) so 1mV becomes 1V but a 1V at Vin+ would saturate the output near V+.

Now imagine the ground at R1 is not 0V and is offset by -1mV, the output will go up by x1000 = 1V. But if both the ground voltage and Vin+ change at the same time. there is no change in Vin+ & Vin- so the OA output stays the same at 0V ( assuming dual supplies or single supply type with rail-to-rail in & out capable), ie. no difference on input so no difference on output. ( as long as you follow the specs for Vin to stay with the supply operating range for Vin {min,max}

So remember the Vin+ always equals Vin- and inverting side Resistor gain is always R2/R1 and the non-inverting gain is the same except positive and = R2/R1+1 then you won't have to do Thevenin equations again.

 

[jasonc2]

Thank you for the reply but I still confuse about the way input see different and amplify it.

This circuit for example.

Let's say if VR1=1/2Vout

When the inputs see a difference, say 1V and 0V, the amp massive gain (say 1000) amplifies the difference(1V).

Now Vout is 1000V, half of this was fed back to the inverting terminal. The inputs will be 1V and 500V, Vi=500-1=499V

Again Vout is 499x1000=499000V. The inputs will be 1V and 499000V.

Why Vout is getting bigger??

Let's say in your example:
Vin = 3
R1 = 47K
R2 = 47K
Op Amp Gain = 200000

Since R1 = R2 we know that VR1 = Vout / 2. We expect this op-amp to produce Vout = 2 * Vin.

Here is what we know:

For an op amp: Vout = (V+ - V-) * Gain (where Vout is output, V+ is + input, V- is - input, Gain is op amp DC gain), so:
V+ = Vin - Because they are connected.
V- = VR1 - Because they are connected and R1's other connection is 0V ground.
Vout = (Vin - VR1) * Gain - This is what an op amp does.
VR1 = Vout / 2 - Because of R1,R2 voltage divider.

Our goal is to calculate Vout. Let's plug in what we know:
-> Vout = (3 - VR1) * 200000
-> Vout = (3 - Vout / 2) * 200000 [substitution]
-> (Vout / 200000) + (Vout / 2) = 3 [algebra]
-> (100001 * Vout) / 200000 = 3 [algebra]
-> Vout = 600000 / 100001 ≈ 5.99994 volts

5.99994 volts is as close as you'll get to the expected 6V output (2 * Vin where Vin = 3). That is the voltage Vout will eventually settle on. To get closer to the target Vout = 2 * Vin you'd want to use an op-amp with a higher gain.

To verify that this makes sense (I'm rounding values here but not in my calculations):
Vin = 3
Vout ≈ 5.99994
VR1 ≈ 5.99994 / 2 ≈ 2.99997
Vin - VR1 = input difference ≈ 0.00003
(Vin - VR1) * Gain = Vout ≈ 0.00003 * 200000 ≈ 5.99994

So you can see that the op amp relation Vout = (V+ - V-) * Gain holds with V+ = 3 and Vout = 5.99994 and V- = Vout / 2.

Keep in mind this doesn't magically happen instantaneously, which I think is the source of a lot of confusion. It converges over time and the maximum rate at which Vout can rise or fall is given by the op-amps slew rate, which is typically in volts per microsecond (i.e. megavolts per second).

I highly recommend reading this: https://www.allaboutcircuits.com/vol_3/chpt_8/4.html (and everything else about op amps in that chapter). It's well written and concise and gives a good starting point.

 

[D.A.(Tony)Stewart]

Power Steering on your car works the same way.
With the differential input being a pressure valve that on the +side is controlled by you rotating the steering wheel and the -side being a ratio of the output hydraulic force on the tie rods to turn the wheels. This gain in force if we consider how much force it takes to turn the steering wheel with one finger and the force required to pivot the front wheels. The steering Pump is like the Op Amp. It does no work i.e. no hydraulic force if the pressure difference is zero between two valves.. +in by you and the negative feedback valve senses the force applied to the front steering links connected to the front wheels on the road. If the pump was to actually have zero offset in sensing this difference, you would never feel the road providing resistance to the steering wheel, so they intentionally create a deadzone where minor input changes are ignored, i.e. it does not activate the hydraulic pump in either direction until this threshold is exceeded and then the wheels will turn proportionally determine by the R ratio in the hydraulic and steering rod lever ratio design. If this negative feedback was removed. The steering wheel would then become a switch at some position where the wheels would swing violently from one side to the other. Without negative feedback there be nothing to compare, it would become as we say in OA's "open loop" gain" which is very high....and not very useful in a linear world... ( unless you are a "comparator ) or live in the digital world.. this is how it works... if less than threshold it is a "0" and great than threshold it is a "1".

When you play around with CMOS inverters, you will find hundreds of books with kewl ways to use them as linear amplifiers. Just like OA's, except the non-inverting input is internal and usually Vcc/2. So you can use them as x1 up to x1000 linear amplifiers, make them input LPF or HPF or diode detectors or one shots or oscillators or photodiode sensors or thermal switches etc.. .. Ok it works but these hex inverters are also "poor man's Op Amps and work great as long as you remember the same rules of feedback ratio, difference voltage on input and stay within the input and output specs for voltage and the threshold on internal reference is less accurate.

 

[crutschow]

You probably didn't look sharp. Vin is the differential OP input voltage, the large 500V term is the feedback generated part. It's surely opposite to Vout in a negative feedback circuit.

You are the one that "didn't look sharp". :wink: The feed back is negative at the negative input, but the input and output voltages are the same polarity for a non-inverting op amp circuit. Otherwise it wouldn't be "non-inverting".

Vin is the input voltage not the differential input voltage. Negative feedback doesn't necessarily mean a negative voltage, it just means that the feedback goes to an inverting input in this case.

 

[jasonc2]

If you are curious, here is a plot from PSpice's TL082/301/TI model configured as a unity gain follower over 4usec with 0.1nsec time step. Granted it's just a model but it does give an idea of the op-amps behavior:



Top left plot shows input voltage (PWL input) and op-amp output vs. time.
Bottom left shows slew rate, note that it is limited to the 13 V/µs max slew rate which you can find in the TL082 data sheet.
Right side is just a zoomed in portion of the top left plot, showing the op amp response curve. Note the overshoot which is also given in the TL082 datasheet, although I did not test to see if PSpice's model agrees with the datasheet here.

The circuit was just a voltage follower:

J

 

[D.A.(Tony)Stewart]

crutchow < you must be new here... I know after a couple months to give FvM wisdom, the benefit of the doubt on wording if it sounds wrong... even if he is correct.

my interpretation of his english...his punctuation is correct and so are the comments.

Vin is the differential OP input voltage

..correct

the large 500V term is the feedback generated part.

correct

It's surely opposite to Vout in a negative feedback circuit.

..
correct. The feedback is opposite to Vout
correct. The feedback is in the negative feedback circuit.
{and of course we all know the negative feedback circuit is connected to Vin-}

But that's ok. I make misteaks too.

 

[FvM]

The point isn't worth to argue much longer.

But the calculation in post #4 simply uses a wrong sign in the expression for the differential input voltage which is (misleadingly) called "Vi" . Did you review the calculation?

I see that I promoted the confusion by writing "input voltage" instead of "differential input voltage".

 

[jasonc2]

BTW to clarify:

Let's say if VR1=1/2Vout

When the inputs see a difference, say 1V and 0V, the amp massive gain (say 1000) amplifies the difference(1V).

Now Vout is 1000V, half of this was fed back to the inverting terminal. The inputs will be 1V and 500V ...

This is where the confusion comes in. The output would not be 1000V, and the inputs would not be 1V and 500V, as time is a factor, the changes are not instantaneous.

For an op amp with 10V/us max slewrate, for a 1V (+) and 0V (-) input, 1 nanosecond later the output would actually be closer to 1ns*10V/1us = 10mV. Now the inputs are 1V(+) and 0.005V(-). This continues until the output converges on an appropriate value, and of course I am talking in discrete terms. Think calculus here.

If the op-amp were to instantaneously adjust its output voltage (which is impossible), then I guess it would oscillate or something? I don't know I'm not that smart. But it's not instantaneous, it's a convergence over time, albeit a very short time.

 

[FvM]

This is where the confusion comes in.

Not only. You are right, that it's absurd to calculate with this voltage levels. With negative feedback in a stable loop, the OP output is only changing continously and the feedback loop will settle to steady state without reaching extreme voltage levels.

But you stopped quoting post #4 just before the actual expression, which turns negative into positive feedback. With it's action, the output voltage always latches into saturation.

 

[jasonc2]

But you stopped quoting post #4 just before the actual expression, which turns negative into positive feedback. With it's action, the output voltage always latches into saturation.

I intentionally stopped there because a) it was already being discussed [and in a manner that I did not care to participate in, and I have nothing new to add] and b) I believe the continuous nature was the more fundamental cause of the original poster's confusion rather than the mix up of gain signs (which is certainly a problem, but an easy problem to correct and not the core of the issue as I see it -- "the output will be 1000V" was the first major issue in that post and the one I am addressing, his calculations after that, while incorrect, were still based on a fundamental misunderstanding, and would have still led to confusion even if the gain sign was correct).

BTW an Excel spreadsheet that simulates an op-amp that I created is attached, albeit with an extremely rough model. The ODS spreadsheet, if you can open it, is the same but also has a graphical chart in it (I had to zip them because xls/ods files are not allowed).

Remember these are VERY rough (you'll notice the oscillation around the settling voltage, because my gain and slew rate are constant and instantaneous).

You may edit the values in green cells:
Vin(t=0) = the initial input voltage
Gain = gain
Slew rate = max slew rate in V/us
R1/(R1+R2) = resistor ratio (set to 1 for unity gain)

Outputs:
Column A = time in microseconds
Column B = Vin[+] (they're all set to B1 but you can change them to simulate changing Vin[+]).
Column C = Vin[-] = Vout * Resistor Ratio
Column D = Vout at that time

Intermediate Values (to simplify my formulas):
Column F = what the output would be if instant change (Vout = (previous_In[+] - previous_In[-]) * Gain)
Column G = minimum actual output based on previous output, max slew rate and time delta
Column H = maximum actual output based on previous output, max slew rate and time delta
Column I = actual output = Column F clamped to range [Column G, Column H]

In OpenOffice with the ODS file the chart on the right will update when you change values.

This is a rough 0.4usec simulation with 1nsec timesteps. You can change the values in column A if you want to change the timesteps. You can copy + paste more rows if you want to increase the simulation time (just make sure the timesteps increment correctly).

J

- - - Updated - - -

Power Steering on your car works the same way.

P.S. OT: Incidentally, as of this morning, the power steering on my car doesn't actually work. I think you jinxed it! :lol: