How does non linearity cause the generation of harmonics

[Nischitha]

Hi,

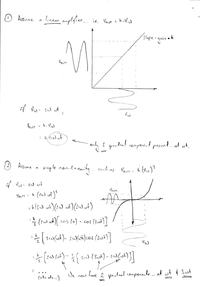
As we know when there is a nonlinear load, the current drawn by the the load is discontinous and it doesnot corresponds to the applied voltage waveform.
But how does this discontinous current or non linearity generate harmonics?

 

[FvM]

I don't know if you like mathematics, but you can reduce the question to a fourier decomposition of non-sinusoidal waveforms into a harmonic series of sine waves. Obviously, the question isn't related to Analog IC design.

 

[thylacine1975]

Yup - perfectly answered by FvM while I was sketching an example

FvM's answer is the general (and "always useful") case - start with an arbitrary signal, and amplify it, subject it to a non-linear load etc. Whatever you do to it, record it (as a function of time). The Fourier transform of your recorded signal will reveal the presence (or absence) of harmonics generated by your non-linear process(es). To address how the non-linear processes produce the hamonics you have to peek at some math. There are numerous ways to do this - here's one (simple) example approach:



Here I've described 'amplification' of an input signal, although the same reasoning applies to voltages developed across nonlinear loads etc. In the case where your amplifier LINEARLY reproduces the input signal, the output is simply a scaled version of the input. We can illustrate frequency domain behaviour while skipping the Fourier decomposition process by assuming a single frequency sinusoidal input Vin = sin(w*t) ; where w = 'omega' = 2*pi*f - the frequency of our virtual sinusoid.

For the linear case, only one sinusoidal component is present in the output... namely the linearly scaled sinusoid that was present at the input. i.e. No harmonics.

Using a (contrived) nonlinear example Vout = k.(Vin)^3 ... [badly approximating a class B amplifier with HEAVY crossover distortion, for example] and applying a set of trigonometric identities, we can see that an output term at (3*w*t) arises - the third harmonic of our input sinusoid.

Needless to say such an example is a gross oversimplification, and real-world non-linearities are rarely represented with simple analytic functions, but it illustrates the point. Substitute a better model of your non-linearity; i.e. Vout = f(Vin) and a large amount of algebraic manipulation later you will have the amplitudes and relative phases of your harmonic terms.

 

[Nischitha]

Mathematically you have shown how harmonics are generated from non linearity. Excellent...
As per the example , 3wt is the 3rd harmonic of the given sinusoid. I agree that this could be explained mathematically.
But I was looking for intitutive meaning of this concept.

Thank you so much...

 

[FvM]

But I was looking for intitutive meaning of this concept.

It's your job to ask clear questions...

By the way what's an intuitive understanding of the term harmonics in your eyes? In my view, a discontinuous waveform is immediately implying harmonic frequencies, without bothering mathematics. You may want to imagine musical sounds. I guess, it's due to a more intuitive view on physical phenomena.

 

[volker_muehlhaus]

Nischitha, try this:

**broken link removed**

 

[Nischitha]

volker_muehlhaus
Thank you