iVenky
Advanced Member level 2

- Joined
- Jul 11, 2011
- Messages
- 584
- Helped
- 37
- Reputation
- 76
- Reaction score
- 35
- Trophy points
- 1,318
- Location
- College Station, Texas
- Activity points
- 6,124
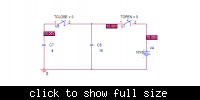
There are two capacitors C1 (4 F) and C2 (16 F). They are separated by a switch. The switch closes at t=0.
When t<0 the voltage in C1 is 10V. What will happen when the switch is closed? What will be the voltage across C1 and C2 now (ie t>0) ?
Thanks in advance.
When t<0 the voltage in C1 is 10V. What will happen when the switch is closed? What will be the voltage across C1 and C2 now (ie t>0) ?
Thanks in advance.