Can anyone explain to me the concept of DFT and FFT please

[mazdaspring]

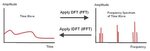
I tried to read the lecture note or lecture video on youtube but it's hard to understand. there are a lot of mathematics but no concept what they are doing and how they work. Anyone please explain to me the concept of it. What are DFT/FFT doing and how they work? or suggest me the source that is easy to understand about this please. Thank you so much.

 

[kak111]

DFT and FFT very simple words , no mathematics


The reason to learn about the DFT and FFT is in order to get a frequency spectrum of a wave
or to understand better what frequencies it is composed of.
This might allow you to better identify, for example, a sound wave that you have sampled
than could be done with the time wave, which is useful for speech recognition.
Or, maybe you want to add or subtract frequencies and recreate the original wave with these
modifications using an inverse fourier transform.
Doing this with light waves you could, for example, remove dirty spots or noise from an image,
or find recurring patterns in an image.


A DFT is a "Discrete Fourier Transform".
An FFT is a "Fast Fourier Transform".
An FFT is a DFT, but is much faster for calculations.
The whole point of the FFT is speed in calculating a DFT.

A Fourier converts a wave in the time domain to the frequency domain.

Every wave has one or more frequencies in it.
An example is a sound wave, if someone speaks, whistles a tune, etc.,
any sample of that sound wave has a set of frequencies that describe the wave.

According to Fourier, you can take a set of sine waves of different amplitudes and
frequencies and sum them up to equal any wave form.
The set of sine waves that is summed up to equal the original wave each has a frequency and magnitude.
A plot of frequency versus magnitude on an x-y graph is a frequency spectrum, or frequency domain, plot.

See Diagram



An inverse Fourier converts the frequency domain components back into the original time wave.

You can reassemble the time wave from the frequency components.

The IDFT below is "Inverse DFT" and IFFT is "Inverse FFT".

A DFT is a Fourier that transforms a discrete number of samples of a time wave and converts it into a frequency spectrum.
However, calculating a DFT is sometimes too slow, because of the number of multiplies required.
And FFT is an algorithm that speeds up the calculation of a DFT. In essence, an FFT is a DFT for speed.

The Discrete Fourier Transform converts discrete data from a time wave into a frequency spectrum.
Using the DFT implies that the finite segment that is analyzed is one period of an infinitely extended periodic signal.

(adapted citation from alwayslearn.com by KAK)

Graph. : FFT of some timewave




The Discrete Fourier Transform (DFT) is one of the most important tools in Digital Signal Processing.

the DFT can calculate a signal's frequency spectrum.
This is a direct examination of information encoded in the frequency, phase, and amplitude
of the component sinusoids.
For example, human speech and hearing use signals with this type of encoding.
Second, the DFT can find a system's frequency response from the system's impulse response,
and vice versa.
This allows systems to be analyzed in the frequency domain, just as convolution allows systems
to be analyzed in the time domain.
Third, the DFT can be used as an intermediate step in more elaborate signal processing techniques.
The classic example of this is FFT convolution, an algorithm for convolving signals that is hundreds
of times faster than conventional methods.



KAK

 

[permute]

one other, possibly helpful observation:

for discrete-time (or discrete-space) signals, it is common to represent the signal as a vector, eg, 1, 2, 3, 4.
the most obvious way to do this is by storing the values as simply 1, 2, 3, 4.

However, this isn't the only way to do this. In the above, the coefficients (1,2,3,4) correspond to a set of basis vectors: (1,0,0,0), (0,1,0,0), (0,0,1,0), and (0,0,0,1).

But this isn't the only choice of basis vectors. the same values could be expressed as:
-1*(1,0,0,0) + -1*(1,1,0,0) + -1*(1,1,1,0) + 4*(1,1,1,1) = 1,2,3,4
Here the coefficients are -1,-1,-1,4.

Another choice might have been:
+4*(1,1,1,1) + -1*(1,0,1,0) + -2*(1,1,0,0) + 0*(0,1,1,0) = 1,2,3,4

or even:
+2.5*(1,1,1,1) + -0.5*(1,-1,1,-1) + -1*(1,1,-1,-1) + 0*(-1,1,1,-1) = 1,2,3,4

The idea is than N data points in a given basis can be transformed into N data points in another basis. The DFT, as an operation, is simply this -- a change of N points equally distributed in time into N points equally distributed in frequency. There are several transforms that can be used to "paint" the N data points using a different set of N "brushes".

As with any transform, there may be some reason for the transform. Obviously the FFT/DFT make a lot of sense for analyzing sine/cosine/periodic functions. In such cases, the coefficients will be sparse -- mostly 0. This would allow for efficient compression, when compression is required -- most of the information from the N points is contained in a fraction of the N points. the DFT/FFT also allow for efficient convolution for the same reasons as the continuous time case.

In general, without a problem, there is no need to perform a transform. The transforms allow for an alternate representation of the signal, and ideally, this representation will be useful for some reason. The exact reason is based on the context. the DFT/FFT are very well known and tend to be useful in many applications. They aren't the only choices.


Not mentioned in the previous post, but from above, an N-point DFT/FFT will give N-points in frequency. This is not the same as a full frequency spectrum. The FFT exploits the fact that, over the N-points in time, all of the basis vectors are periodic (repeat an integer number of times). As a result, any waveform that is not periodic will not be represented exactly by any single basis vector (any single frequency that is periodic in N samples). One frequency will be closest, and will describe most of the signal, but not all. The remaining portion of the signal will be spread out to the other basis vectors in some manner. This will affect the "frequency resolution" in that very closely spaced sinusoids will simply result in a high value for a single basis vector.

One outcome of this effect is that oversampling will not improve frequency resolution. It will increase the analyzed bandwidth. To increase the frequency resolution, data must be taken over a longer interval of time. This in turn reduces the "temporal resolution", as it now takes a long time to get an estimate. This is not processing time. A common misconception is that either increasing the processing or sampling speed will result in a significant increase in frequency resolution. This is only true in cases where processing speed is so limited that data must be dropped.

 

[mazdaspring]

@kak111

Thank you so much. This is very clear to me. I am learning OFDM so I need to understand DFT,FFT.
I have a question here.

Regarding an example of DFT on your website. When you work out on the DFT equation, you get
F(0)=0
F(1)=-2j
F(2)=0
F(3)=2j

What is the benefit of this calculation. When will you use it? Since I see that you will use the data in the graph result to determine the transmitted wave.
How will we use F then?

----------------------------------------------
In my area of study (OFDM), we will use DFT/IDFT or FFT/IFFT to transform the signal from frequency domain to Time domain. and in receiver FFT will be used to transform signal in time domain to Frequency domain so that we can determine the transmitted signal. However I don't know how can you form or determine the original signal from the FFT graph result. Because from the graph you will know only the the set of frequencies of that signal and its amplitude.
e.g. x(t)=cos(2pi*f1*t)-2cos(2pi*f2*t)+4cos(2pi*f3*t)
f1=1,f2=3,f3=5

When we get fourier transform graph, we will see frequency spectrum at 1,3,5 Hz with amplitude 1,2,4 respectively

But how can we know that the original signal is combined with 3 cosine wave above instead of 3 sine wave. How can we know it's cosine or sine.
Also the coefficient of the second wave is -2 but the spectrum shows 2...how can we know it's -2
Could you please clarify this for me. Thank you so much.

---------- Post added at 09:42 ---------- Previous post was at 09:14 ----------

@permute

Thank you so much as well for your reply. I am trying to understand it. By the way, could you please let me know how this can be a vector -->(1,0,0,0)
As I know vector is ai+bj+ck...so it should be (a,b,c)
How can it has 4 components.

I am sorry if this sounds too basic question but I don't get it. Please explain to me. thank you so much.

 

[permute]

you probably should have learned fundamentals of signals and systems and linear algebra before digital communications.

in linear algebra, a vector has no specific interpretation. It can be of any dimension. for example, if you have a 1 second of audio that was sampled at 192ksps, then you could express that as a vector with 192,000 elements. The basis associated with this vector is assumed to be (1,0,...) (0,1,....) ... (0,0,... 1). These basis vectors have the meaning: (1,0, ...) is the basis corresponding to "first sample". (0,1, ...) corresponds to "second sample", etc...

The FFT then performs a transform to a different basis. one where the basis vectors correspond to things like "0Hz", "1Hz", etc...

 

[kak111]

Hello again.
I´m a bit busy with jobs, but here is something.............

F(0)=0
F(1)=-2j
F(2)=0
F(3)=2j

Answer is here
The DFT

How can we know it's cosine or sine.




We get now separated frequencies and amplitudes in FFT spectrum
without their phase differencies.

For phases and amplitudes we need count separate FFT spectrum



Or real and imagimary part separate FFT spectrum etc.............



This is one of the best free book in web

The Scientists and Engineer's Guide to DSP.

You can browse and/or download the entire book without charge
» Browse and/or download chapters from the book
» Copyright and permissible use

The Scientist and Engineer's Guide to Digital Signal Processing's Table of Content

Here is lessons and lectures

‪fourier series‬‏ - YouTube

‪fourier analysis‬‏ - YouTube

KAK

Ps. Other interesting about dft and fourier series.....................

Search Results - fourier - Wolfram Demonstrations Project

Fast Fourier Transform Calculator

**broken link removed**

**broken link removed**

Try FFT analyzer

Java FFT Analyzer

 

[TimMiller]

the DFT/FFT are very well known and tend to be useful in many applications. They aren't the only choices.

permute,

Could you name the other possible alternatives for finding frequency of a signal? I am a first year graduate student in biomedicine and has just touched this topic. There are many other mathematical transforms besides DFT, like wavelet transform, discrete cosine/sine transform, Hankel transform, Z transform, etc. Which of them can also be used for frequency determination?

Could you have a look at post How many ways to determine signal frequency?


Tim

 

[iVenky]

I believe most of us are good in practical but when it comes to theoretical no one understands. It's essential that you should have a sound theoretical knowledge. The main reason why we don't understand theory is because of the mathematics involved in it which makes it very difficult to understand intuitively. I believe that standard books like "Digital Signal Processing" by Oppeheim or Proakis don't deal much about the intuitive part of the subject. They rather deal with very difficult mathematical symbols and formulae.

Every signal is made of infinite number of sinusoidal waves with different frequencies. Each frequency has it's own amplitude. So if you want to learn about the frequency spectrum of a signal it's necessary that you should need a function which deals explicitly with frequency. DFT is used for this operation.

I cannot write everything that I had learnt in just one paragraph. Refer these books ---"Scientists and Engineers guide to DSP" by Steven W. Smith.
See more about Laplace transforms before you see fourier-- For laplace transforms the best book is "Engineering Circuit Analysis" by William Hayt. This is the best book I have seen because you will understand everything intuitively.

 

[crazyboy]

Hi friends, I'm a newbie to this form. I read this form on many questions and find it very important. I have a basic question on FFT. As we know that FFT of a sine wave will be a double delta functions one at +ve frequency and the other at -ve frequency over imaginary axis (based on theoretical calculation of Fourier Transform). But when I tried to simulate FFT of a sine wave its showing the result on the real axis? or imaginary axis? a bit confused with this. Any help is highly appreciable.