michaelhust
Junior Member level 1

- Joined
- Sep 30, 2011
- Messages
- 15
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1,281
- Activity points
- 1,404
Hi, everyone!
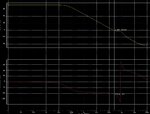
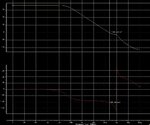
For the op-amp compensated in the way as follows, there is a RHP zero a LHP zero lower than the nondominate pole.
That makes it difficult to compensate , so i wonder which position introduces the zeroes and whether there is someway to modify the zeroes to a higher position.
Thanks for your advice!
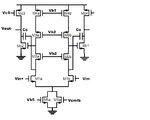
For the op-amp compensated in the way as follows, there is a RHP zero a LHP zero lower than the nondominate pole.
That makes it difficult to compensate , so i wonder which position introduces the zeroes and whether there is someway to modify the zeroes to a higher position.
Thanks for your advice!

Last edited: