tahir4awan
Full Member level 4

Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.






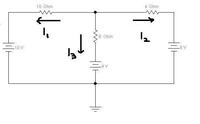
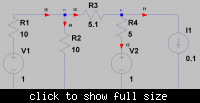


so when you denote the currents direction you must keep in there is at least one current is going out of node ,and at least one current leaving it






