Is Razavi's book wrong about this current mirror?

example 11.1 of Razavi's "Design of analog cmos integrated circuits" is about this current mirror.

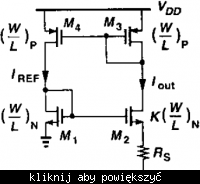
He estimates the change in Iout for a small change in supply voltage.
He uses an expression from Chapter 3 of that book to write \[G_{m2} = {{I_{out} } \over {V_X }}\]

The problem is, eq. 11.7 is derived for a case where drain of CS transistor is grounded; While in this current mirror drain of M2 is connected to a resistor (R3)

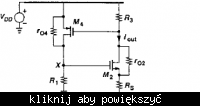
Is it correct to use equation 11.7 in this example?

spur said:

The problem is, eq. 11.7 is derived for a case where drain of CS transistor is grounded

Click to expand...

I wouldn't think so: Iout in Fig. 3.17 (p. 61) is a current source with (infinitely) high resistance. Otherwise the following equations (3.52 .. 3.55) wouldn't make sense.

spur said:

Is it correct to use equation 11.7 in this example?

Click to expand...

Yes, I think so.

Hi.

spur, I think your doubts are reasonable and equation 11.7 is indeed incorrect (but it can be applied in this case). I'll try to show this using two-port equivalent model of the the common-source amplifier with source degeneration (attached figure).

Ro is output resistance (3.59), Gm is transconductance (3.55), Rdrain - resistor connected to the drain. Iout1 is output current with short-circuited output (Iout1 = Gm*Vx). Iout in the Figure 11.4 can be identified as Iout2. Using equation for current divider: Iout2 = Iout1*Ro/(Ro+Rdrain) = Gm*Vx*Ro/(Ro+Rdrain). Gm in the example 11.1 is defined as Iout/Vx (Iout2/Vx). Using previous equation we get Gm(11.7) = Gm(3.55)*Ro/(Ro+Rdrain). Thus when Rdrain has order of magnitude comparable with that of Ro equation 11.7 will give significant error. But in the example 11.1 Rdrain (R3) is resistance of diode-connected transistor (1/gm3) and in most cases Ro >> R3 = Rdrain, which means that Gm(11.7) = Gm(3.55).

i agree there's an error...but the problem is that razavi says that the sensitivity vanishes for ro4->infinity.

doing the small signal equivalent i had that the potential of the drain of M2 is simply (is it right?) Vdd-Iout*R3 (where R3 is the resistance of the diode connected M3). From this potential i calculated the sensitivity without any approximation:

Iout/vdd = (1+ gm2 r02*(R1||r04)/r04) / (r02 + Rs + R3 + r02 gm2 Rs - gm2 * r02 * R3 * gm4 *(R1||r04)/r04) )

and, even if ro4=infty, i have a non zero-sensitivity.

am i wrong?


ps R1 is the resistance of diode connected M1.