Aya2002
Advanced Member level 4

Hi experts, i have a quistion here, please read the following paragragh as it is in a pdf document on the web:
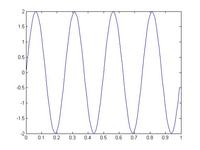
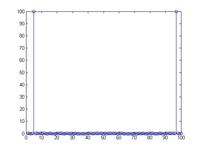
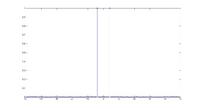
The Fourier transform can be computed using the Matlab code
Fk = fft(fn)/N; % The FFT of the signal fn
fn = ifft(Fk)*N; % The Inverse FFT
ifft(fft(fn)); % This result = fn (within machine precision)
We must divide by the number of grid points N if we want to use the results of the FFT, because Matlab puts the normalization only in the inverse transform. As a result we must then multiply the IFFT by N to counter Matlab's dividing by N.
my doubt is: is the above is correct?
Thank you in advance.
Added after 3 hours:
any reply please
The Fourier transform can be computed using the Matlab code
Fk = fft(fn)/N; % The FFT of the signal fn
fn = ifft(Fk)*N; % The Inverse FFT
ifft(fft(fn)); % This result = fn (within machine precision)
We must divide by the number of grid points N if we want to use the results of the FFT, because Matlab puts the normalization only in the inverse transform. As a result we must then multiply the IFFT by N to counter Matlab's dividing by N.
my doubt is: is the above is correct?
Thank you in advance.
Added after 3 hours:
any reply please