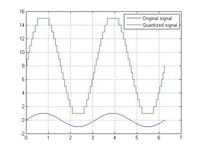
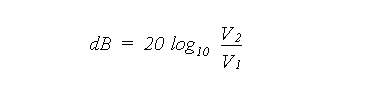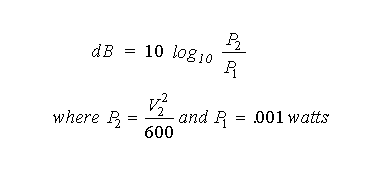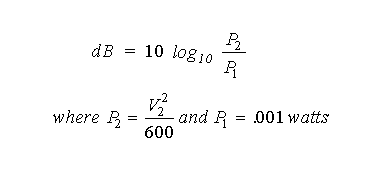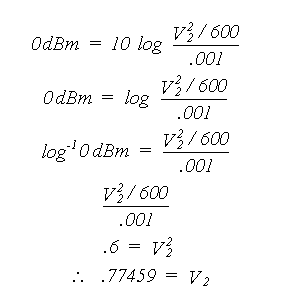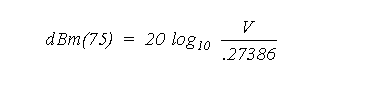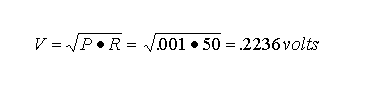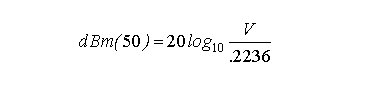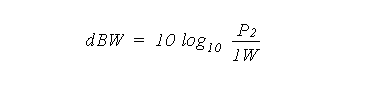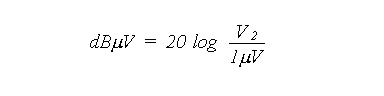Aya2002
Advanced Member level 4

- Joined
- Dec 12, 2006
- Messages
- 1,140
- Helped
- 184
- Reputation
- 376
- Reaction score
- 117
- Trophy points
- 1,343
- Location
- Iraq
- Activity points
- 8,006
Sampling
---------------------------
Converting an analog signal to a digital one is a necessary step for a computer to
analyze a signal: modern computers are digital machines, and can store only digital values.
In the continuous function x(t), we replace t, the continuous variable, with nTs, a discrete value. We use n to index the discrete array, and Ts is the sampling period, the amount of time between two samples. The sampling time is the inverse of the sampling frequency fs, that is, Ts = 1/fs.
Before we can talk about sampling, let us call the frequency range of the signal
that we are interested in the bandwidth. Sometimes, we simply use the highest
frequency as the bandwidth, implying that we are interested in all frequencies between 0 Hz and the maximum. Other times, it may be limited, e.g., the visible light spectrum.
The term critical sampling applies to the case when the sampling rate is exactly twice the bandwidth, B. This means that we will record the signal just fast enough to properly reconstruct it later, i.e., fs = 2B. We get this value based on Nyquist's criterion, fs ≥2B, and choosing the lowest possible sampling frequency.
Oversampling is taking samples more frequently than needed (or more than 2 times the bandwidth). This results in more samples than are needed. You can use oversampling, but you may not want to due to hardware limitations, like not being able to process it fast enough, or not being able to store it in memory. Oversampling may be something you would want to do if you are working with cheap hardware, such as an inexpensive digital-to-analog converter, which appears to be the case with CD players. An inexpensive digital-to-analog converter may use a simple step function to recreate the signal. Therefore, the more samples it has to work with, the smaller the time between the samples, and the better it approximates the original. As a counter example, reading (and storing) the temperature every microsecond would produce a massive volume of data with no gain for predicting tomorrow's weather.
Undersampling occurs when we do not take samples often enough, less than twice the bandwidth. You would not want to use this, since you cannot reconstruct the signal. Also, any analysis done on an undersampled signal will likely be erroneous (as we say in computer programming, \garbage in, garbage out").
x[n] = x(nTs) describes the sampling process. Ts is the sampling time, while
n is an index. This means that the continuous signal x is converted into a digital
representation. x[n] is not exactly the same as x(t). It cannot be, since x(t) is
continuous. At best, x[n] is a good approximation of x(t).
The period of a signal is the length of time before it repeats itself. For a sinusoid,
we only need to know the frequency f, since we define the period as T = 1/f .
Example:
If we used x(t) below and sampled it at 20 kHz, how many samples would we have
after 60 ms?
x(t) = 3 cos(2Π404t +Π/4) + 2 cos(2Π6510) + cos(2Π660t -Π/5)
Answer:
The first thing to notice is that the number of samples really does not depend on
the signal itself. That is, all we need to answer this question is the 20 kHz sampling
rate (fs) and the total time 60 ms.
The sampling period is 1/(20 kHz) or 1/(20,000 Hz). Since Hz is in cycles/sec,
1/Hz would be sec/cycles, or just seconds. We take the first sample at time = 0,
then wait 1/(20,000) sec, and take another, and continue until 60 ms = 0.060 seconds is up.
To find the numerical answer, multiply 0.060 by 20,000, then add 1 (since the
first sample was taken at time 0). For answering this (or any) question on a test,
it is important to show your thought process. A good answer would include the
analysis (and wording) as above.
Thanks
---------------------------
Converting an analog signal to a digital one is a necessary step for a computer to
analyze a signal: modern computers are digital machines, and can store only digital values.
In the continuous function x(t), we replace t, the continuous variable, with nTs, a discrete value. We use n to index the discrete array, and Ts is the sampling period, the amount of time between two samples. The sampling time is the inverse of the sampling frequency fs, that is, Ts = 1/fs.
Before we can talk about sampling, let us call the frequency range of the signal
that we are interested in the bandwidth. Sometimes, we simply use the highest
frequency as the bandwidth, implying that we are interested in all frequencies between 0 Hz and the maximum. Other times, it may be limited, e.g., the visible light spectrum.
The term critical sampling applies to the case when the sampling rate is exactly twice the bandwidth, B. This means that we will record the signal just fast enough to properly reconstruct it later, i.e., fs = 2B. We get this value based on Nyquist's criterion, fs ≥2B, and choosing the lowest possible sampling frequency.
Oversampling is taking samples more frequently than needed (or more than 2 times the bandwidth). This results in more samples than are needed. You can use oversampling, but you may not want to due to hardware limitations, like not being able to process it fast enough, or not being able to store it in memory. Oversampling may be something you would want to do if you are working with cheap hardware, such as an inexpensive digital-to-analog converter, which appears to be the case with CD players. An inexpensive digital-to-analog converter may use a simple step function to recreate the signal. Therefore, the more samples it has to work with, the smaller the time between the samples, and the better it approximates the original. As a counter example, reading (and storing) the temperature every microsecond would produce a massive volume of data with no gain for predicting tomorrow's weather.
Undersampling occurs when we do not take samples often enough, less than twice the bandwidth. You would not want to use this, since you cannot reconstruct the signal. Also, any analysis done on an undersampled signal will likely be erroneous (as we say in computer programming, \garbage in, garbage out").
x[n] = x(nTs) describes the sampling process. Ts is the sampling time, while
n is an index. This means that the continuous signal x is converted into a digital
representation. x[n] is not exactly the same as x(t). It cannot be, since x(t) is
continuous. At best, x[n] is a good approximation of x(t).
The period of a signal is the length of time before it repeats itself. For a sinusoid,
we only need to know the frequency f, since we define the period as T = 1/f .
Example:
If we used x(t) below and sampled it at 20 kHz, how many samples would we have
after 60 ms?
x(t) = 3 cos(2Π404t +Π/4) + 2 cos(2Π6510) + cos(2Π660t -Π/5)
Answer:
The first thing to notice is that the number of samples really does not depend on
the signal itself. That is, all we need to answer this question is the 20 kHz sampling
rate (fs) and the total time 60 ms.
The sampling period is 1/(20 kHz) or 1/(20,000 Hz). Since Hz is in cycles/sec,
1/Hz would be sec/cycles, or just seconds. We take the first sample at time = 0,
then wait 1/(20,000) sec, and take another, and continue until 60 ms = 0.060 seconds is up.
To find the numerical answer, multiply 0.060 by 20,000, then add 1 (since the
first sample was taken at time 0). For answering this (or any) question on a test,
it is important to show your thought process. A good answer would include the
analysis (and wording) as above.
Thanks