powersys
Advanced Member level 1

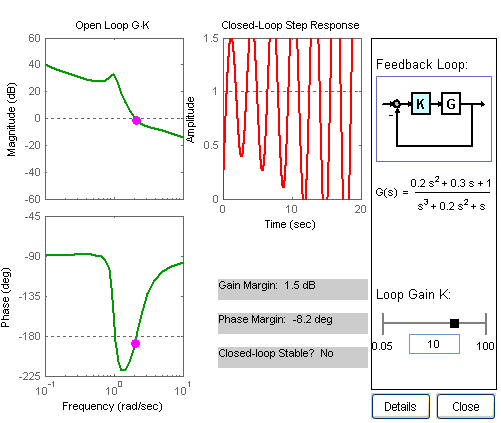
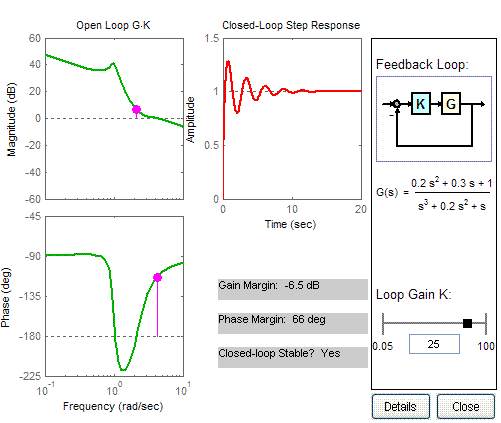
bode plot cross frequency
Bode plots:
1) Magnitude vs frequency
2) Phase vs frequency
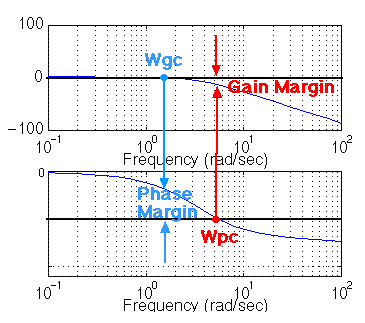
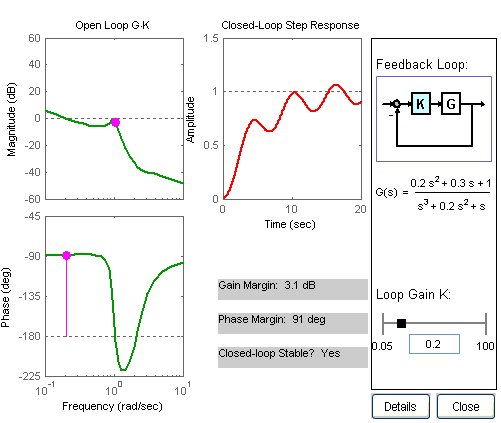
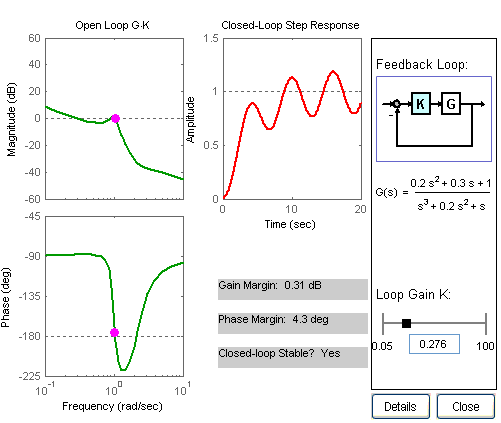
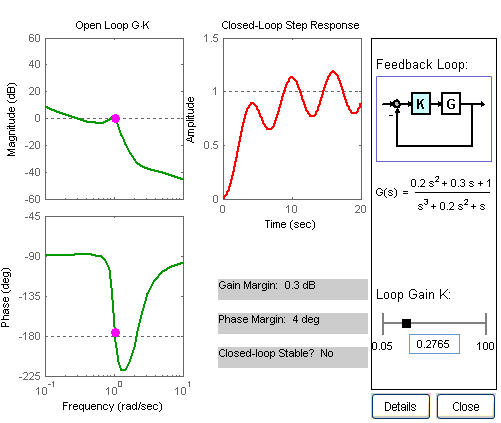
How do we determine, from BODE plots, that a system is stable or not?
Revised Bode Stability Criterion
**broken link removed**
Bode plots:
1) Magnitude vs frequency
2) Phase vs frequency
How do we determine, from BODE plots, that a system is stable or not?
Revised Bode Stability Criterion
**broken link removed**