Zebra123
Newbie

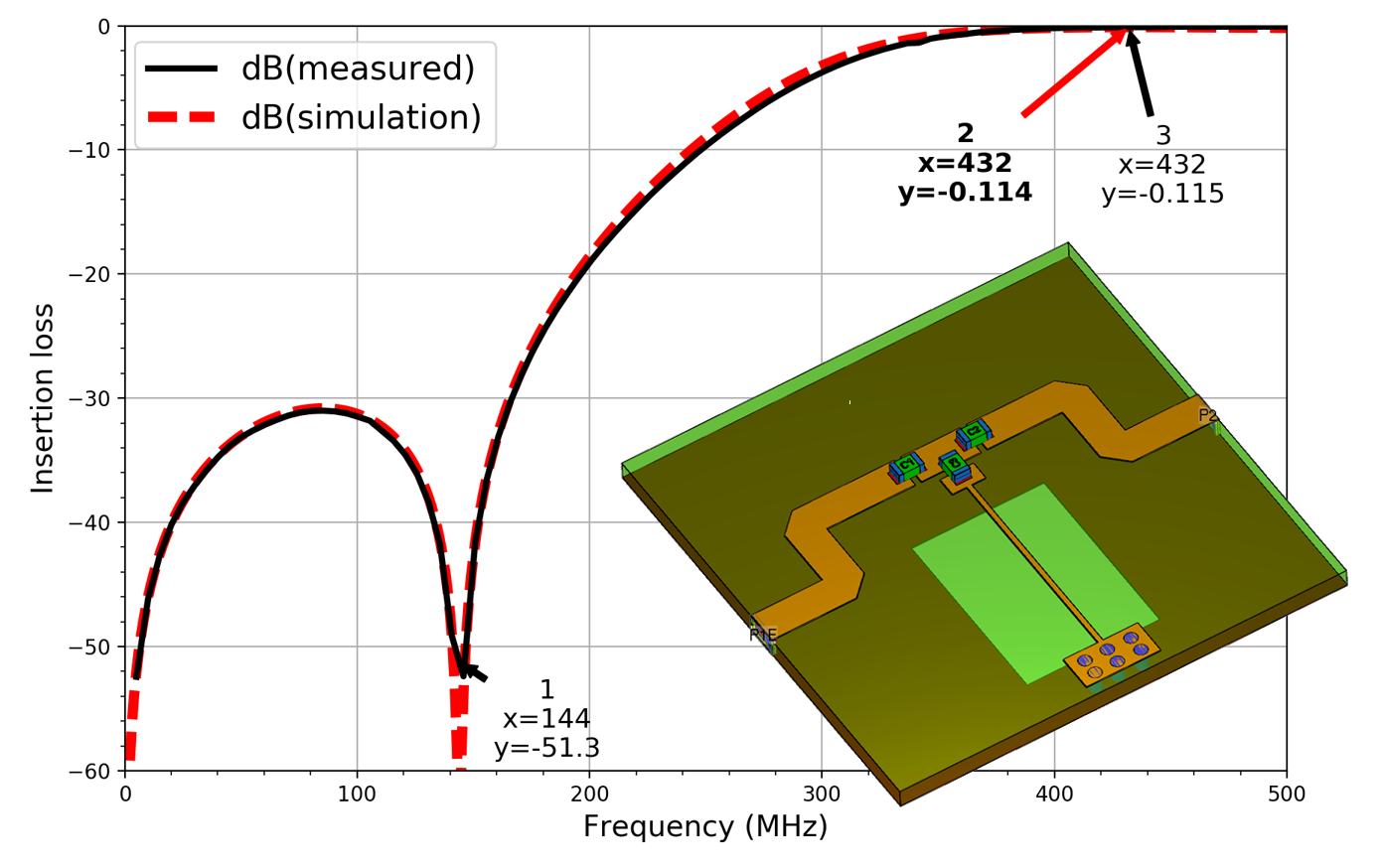
As mentioned in the application Note:

And the explanation:

Alright, the additional 1mm trace can be regarded as part of the matching network, suppressing harmonic levels.
However, a chip inductor also achieves this goal, doesn’t it?

Design Flexibility:
You can change the inductor value, such as 0.5nH, 1nH, 1.5nH……
But the parasitic inductance of the additional 1mm trace is unalterable until you modify the layout.
In addition, even though we have simulation tool, it is difficult for us to decide the actual value of the parasitic inductance precisely.
Thus,
chip inductor wins much!!
Layout space:
The length of the 0201 sized chip inductor is 0.6mm

And this saves layout space more than the additional 1mm trace.
Thus,
chip inductor wins !!
BOM Cost
Sure, the parasitic inductance method can save BOM cost because we can eliminate a chip inductor.
However, I don’t think it saves BOM cost dramatically to eliminate a chip inductor.
Thus,
The parasitic inductance method wins by a little!
Consequently, I wanna realize the big advantage of the parasitic inductance method.
I’ve asked chatGPT, but it didn’t give me a satisfactory answer.
Can someone explain the method further?
Thanks!!
And the explanation:
Alright, the additional 1mm trace can be regarded as part of the matching network, suppressing harmonic levels.
However, a chip inductor also achieves this goal, doesn’t it?
Design Flexibility:
You can change the inductor value, such as 0.5nH, 1nH, 1.5nH……
But the parasitic inductance of the additional 1mm trace is unalterable until you modify the layout.
In addition, even though we have simulation tool, it is difficult for us to decide the actual value of the parasitic inductance precisely.
Thus,
chip inductor wins much!!
Layout space:
The length of the 0201 sized chip inductor is 0.6mm
And this saves layout space more than the additional 1mm trace.
Thus,
chip inductor wins !!
BOM Cost
Sure, the parasitic inductance method can save BOM cost because we can eliminate a chip inductor.
However, I don’t think it saves BOM cost dramatically to eliminate a chip inductor.
Thus,
The parasitic inductance method wins by a little!
Consequently, I wanna realize the big advantage of the parasitic inductance method.
I’ve asked chatGPT, but it didn’t give me a satisfactory answer.
Can someone explain the method further?
Thanks!!