step response of a low pass LC filter

so I have a LC low pass filter and I give it a step input like so in LTSpice



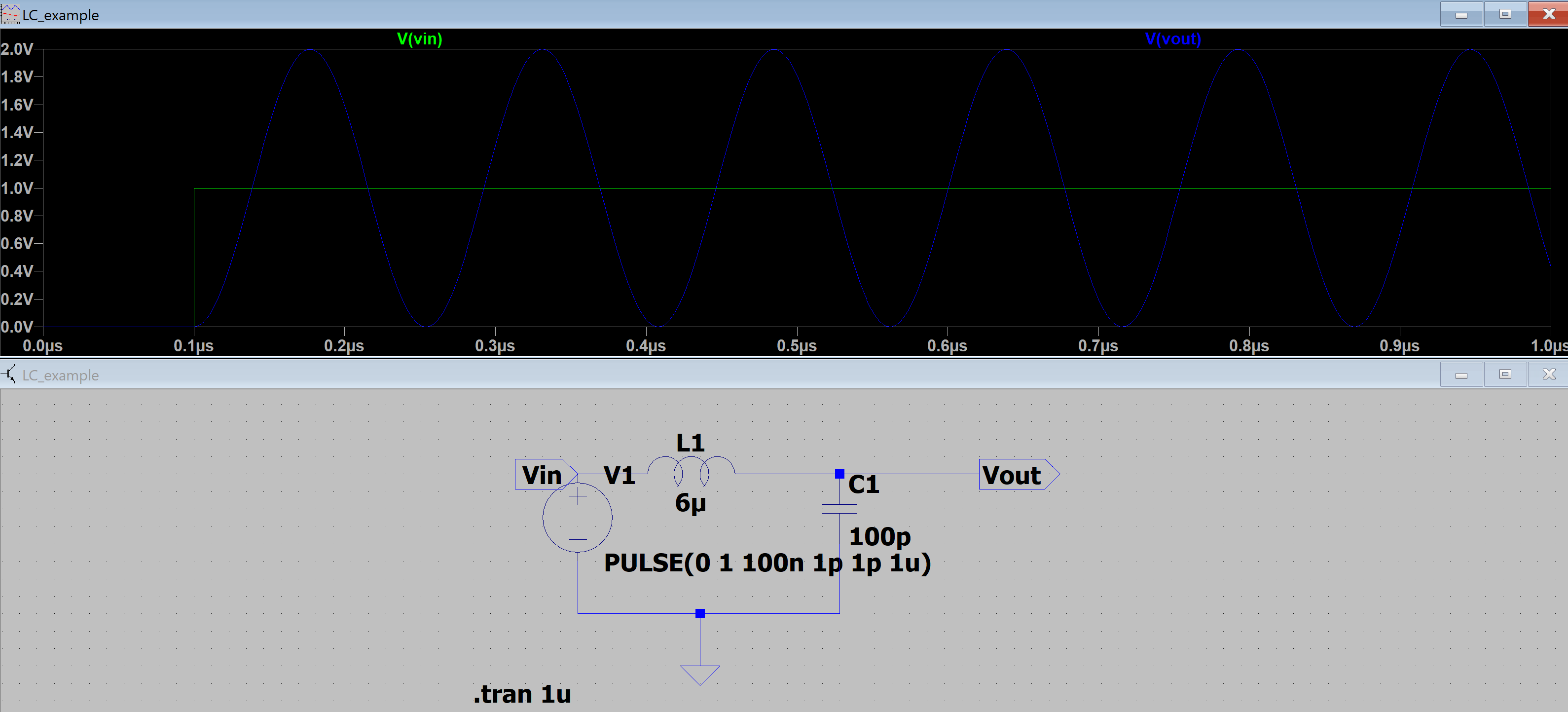
Now the inductor and capacitor are ideal with very high Q and no parasitic R. So the resulting Vout is a sine wave oscillating at the resonant frequency. My question is why does the amplitude of the sine wave go as high as 2V for a 1V step input?

I want to understand, intuitively, why the voltage on the cap increases to 2V at its peak.

The circuit with infinite Q is no useful filter.

Consider that the average voltage across an inductor is zero. Respectively Vout average is 1V. If the oscillation goes down to 0V, it must also go up to 2V.

Why does your ground node ref symbol appear to be unconnected ?


Regards, Dana.

FvM said:

The circuit with infinite Q is no useful filter.

Consider that the average voltage across an inductor is zero. Respectively Vout average is 1V. If the oscillation goes down to 0V, it must also go up to 2V.

Click to expand...

Hello FvM

If I understand you right, since average voltage across inductor is zero (or average inductor current is constant), we have
Vin - Vout for one half cycle equal to Vin - Vout for another half cycle

Initially it is 1 - 0 = 1V so second half cycle it is 1V - 2V = -1V. Add the two and you get 0V avg.

Unloaded two pole filter is undamped. Zero source load and infinite output load. It will just ring at resonance of LC when hit with a pulse.

tenso said:

why the voltage on the cap increases to 2V at its peak.

Click to expand...

If you apply a step input voltage to an LC tank, the inductor current increases until the capacitor voltage equals the input step voltage and there is no voltage across the inductor.
But due to the inductance of the inductor, the current does not stop flowing into the capacitor.
The stored inductive energy keeps the current flowing, increasing the capacitor voltage as the inductor current gets smaller, until all the inductive energy is stored in the capacitor and the current stops.
It turns out that ideally, the capacitor voltage will always be twice the input voltage at that point.

I will leave the mathematical proof of that. using a little calculus, as an exercise for the reader.

Below is the simulation showing the described relationship between the inductor current (red trace) and the capacitor voltage (yellow trace).

as the cap charges energy is stored in the L by way of rising current - when Vcap = Vinput, the charged inductor now delivers all its energy into the cap - for an unloaded system with no losses - it just so happens than the energy in the L is enough to cause Vcap-final = 2 x Vin ... it is to do with the fact that the ckt rings at the natural resonance freq, where 1/2piFC = 2piFL as a result the energy stored in either is the same, hence 2 x Vin ...

crutschow said:

If you apply a step input voltage to an LC tank, the inductor current increases until the capacitor voltage equals the input step voltage and there is no voltage across the inductor.
But due to the inductance of the inductor, the current does not stop flowing into the capacitor.
The stored inductive energy keeps the current flowing, increasing the capacitor voltage as the inductor current gets smaller, until all the inductive energy is stored in the capacitor and the current stops.
It turns out that ideally, the capacitor voltage will always be twice the input voltage at that point.

I will leave the mathematical proof of that. using a little calculus, as an exercise for the reader.

Below is the simulation showing the described relationship between the inductor current (red trace) and the capacitor voltage (yellow trace).

View attachment 163709

Click to expand...

Hi, thanks for taking the time to answer. Any hint as to how show this mathematically? I know we consider the average current across L is constant so the average voltage across it is zero.

This might help -



Regards, Dana.