circuitking
Full Member level 5

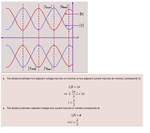
On a transmission line, if we take standing wave then the distance between two voltage maxima or minima is lamda/2, which is 360°. So lamda equal to 720° degree on smith chart. But if I have to calculate physical length of the line, I ll follow this.
Say electrical length BL =30 then
360°-->lamda,
30°--->30°*(lamda/360) so L=lamda/12. So here I am using 360° as lamda. Where am I making mistake?
Say electrical length BL =30 then
360°-->lamda,
30°--->30°*(lamda/360) so L=lamda/12. So here I am using 360° as lamda. Where am I making mistake?