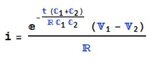sassyboy
Full Member level 1

- Joined
- Sep 20, 2003
- Messages
- 98
- Helped
- 28
- Reputation
- 56
- Reaction score
- 13
- Trophy points
- 1,288
- Location
- United Kingdom
- Activity points
- 1,426
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.





Hi. I thought the energy stored calculated in part (a) would be the final energy stored.
However, the textbook's answer indicate part (a) is 11mJ and part (c) final energy stored = 7.6mJ.
Please help! What is my misconception in this case?
View attachment 149877



An oscillation starts, and the energy disappears gradually via resistive losses and electromagnetic radiation.
The dielectric of a capacitor does not store energy.


A circuit containing only C (or even and RC element) cannot produce oscillation. However, a single current pulse can produce some electromagnetic radiation.
Energy does not disappear just like that; it does get converted into heat and is dissipated (adds to entropy). But what happens if there is no resistance present at all?
Are you suggesting that the principle of conservation of energy does not apply to electronic circuits?

A detailed discussion can be found e.g. here https://en.wikipedia.org/wiki/Two_capacitor_paradox...

Hi. I thought the energy stored calculated in part (a) would be the final energy stored.
However, the textbook's answer indicate part (a) is 11mJ and part (c) final energy stored = 7.6mJ.
Please help! What is my misconception in this case?
View attachment 149877

Pardon my ignorance, I did not know that it is a burning issue. Let me present my solution in brief, without equations and complex solutions (sometimes descriptive ideas catch the mind easily):
1. Simplify the problem and reduce to basic essentials: consider an ideal capacitor charged to a voltage V being shorted by a wire of negligible resistance.
2. To get some idea fixed, consider some small but finite resistance: all the energy is dissipated in the resistance. After all, this is how capacitative discharge is used in cars and also in welding!
3. Consider now the resistance of the wire is being reduced to zero. What happens to the energy now?
4. There is some displacement current flowing through the capacitor dielectric. When the capacitor is charged, the dielectric is polarised (low entropy) and the external current is infinite and the dielectric is now returns to unpolarised state (high entropy)
5. Hence when a capacitor is shorted, the dielectric dissipates all the energy.
6. Consider a parallel plate capacitor with vacuum as the dielectric. There is no dipole to orient or disorient now.
7. The electric field collapses rapidly and that produces a burst of electromagnetic radiation.
8. The displacement current (during the discharge of the capacitor) is not infinite because Maxwell's law. The electromagnetic waves can be detected with a shortwave radio.
9. This remains valid even in absence of parasitic elements.
Thermodynamically speaking, this is an irreversible process and energy is lost to entropy. However, if you connect an ideal motor in the discharge circuit, you can recover all the "lost" energy.

Hi,
Actually, the textbook is correct.
The energy here is a function of two factors: the square of the voltage and the capacitance. Remember (1/2)*C*V^2?
The initial energy is the energy in the 220uF capacitor at 10V and that energy is W = (1/2)*C*V^2 = 0.5*220u*10^2 = 11mJ. That is the solution to the (a) part. Here the 220uF-capacitor is fully charged so the capacitance is 220uF.
For the (c), the energy drops not because of anything else but because the charges that 220uF-capacitor stored at 10V is now contained in a larger vessel (ie 220uF+100uF = 320uF-capacitor). The misconception here is due to the fact that we often are not able to differentiate between capacitance and capacitor.
Capacitance is actually a measure of the amount of charges that a capacitor can store per unit of voltage (C = q/V) whereas a capacitor is just a vessel for storing charges. What (c) is really asking of you is what the energy would be if this same quantity of charges were contained in a larger vessel. Realize that when the 220uF-capacitor is expanded to a 320uF-capacitor (ie 220uF+100uF) no charge is lost or gained but the voltage drops and that the energy W is a function of a square of this voltage.
To get the energy is quite simple:
W/11mJ = 220uF/(220uF+100uF)
:. W = 11mJ*220/320 = 7.5625mJ.
- - - Updated - - -
Let me explain the solution to part (c) a little further, mathematically.
Given:
V1 = 10V
C1 = 220uF
C2 = 220uF + 100uF = 320uF
Now,
C1*V1 = Q = C2*V2
Q = C1*V1 = 220uF * 10V = 2200uC
Q = C2V2
2200uC = 320uF * V2
V2 = 2200uC/320uF = 6.875V
W2 = (1/2)*C2*V2^2 = 0.5 * 320uF * 6.875^2
W2 = 7.5625mJ.

Charged:-----When you say a cap is charged, what is it charged with? For every electron that enters a capacitor lead at one end, a matching electron exits the opposite lead. Therefore, a cap with a 1000 volts across it has the same net number of electrons as a cap with no voltaqe across it, namely zero net change of charge. The cap is being "charged" with energy when a voltage is applied across it, so you might as well say the cap is being energized.
For every electron that enters a capacitor lead at one end, a matching electron exits the opposite lead.
Yet torque and work are two different physical entities.





If I am to measure the energy stored in a capacitor, but I have no joulesmeter (it broked), then how should I go about with this practical experiment.