Eshal
Advanced Member level 1

- Joined
- Aug 29, 2012
- Messages
- 470
- Helped
- 16
- Reputation
- 32
- Reaction score
- 15
- Trophy points
- 1,298
- Location
- Nowhere :)
- Activity points
- 5,149
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.




-235° is equal to 55°

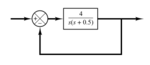
sorry, didn't get it.anyway for now i can tell that the 2.38 comes like the 8.34



180-235=-55
This is angle deficiency. It means +55 must be compensate by ZERO. I hope you know what are poles and zeros in control system
sorry, didn't get it.


no no.. it is just a lead-lag compensator using root locus approach. I just want to know how does 2.38 come? Because in the attached image in post#1, they say by using simple trigonometry. But how?


ok fine :'(




