neazoi
Advanced Member level 6

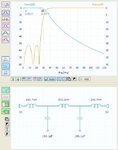
Hello, can you please help me design a LPF for 25MHz (50R)
I need it to be quite sharp, in the sense that I need to attenuate the >= 28MHz quite a lot.
Thanks
I need it to be quite sharp, in the sense that I need to attenuate the >= 28MHz quite a lot.
Thanks