[SOLVED] Why is Quantization noise spectrum from -fs/2 to + fs/2 ?

Hi.

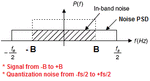
Can somebody please explain (maybe in a little layman's terms ;-)) the physical significance of WHY the ADC quantization noise spectrum lies from -fs/2 to + fs/2 (fs being the sampling freq)?

**broken link removed**

-- is it like the max. possible freq of such noise always in that range?

Thanks!

Hi,

The quantization noise is in the range -fs/2 to fs/2 because ALL the frequency content of the digitized signal lies in that range. Any frequency content outside of the the range -fs/2 to fs/2, also known as the Nyquist interval, is aliased, or folded back into the Nyquist interval.

Thanks..

Is it so that quantization (preceded by sampling) causes the "quantization noise" to be confined in the range of -fs/2 to + fs/2 ?

jdp721 said:

..............
Is it so that quantization (preceded by sampling) causes the "quantization noise" to be confined in the range of -fs/2 to + fs/2 ?

Click to expand...

Don't understand your question.

The act of sampling generates quantization noise due to the finite amplitude steps in the sampling process. This bandwidth of this noise and the sampled signal bandwidth, goes from -fs/2 to +fs/2 as determined by the Nyquist theorem. The bandwidth of the two are the same because the sampling frequency is identical for both.

crutschow said:

.... The bandwidth of the two are the same because the sampling frequency is identical for both.

Click to expand...

Please don't mind me elaborating a bit

Say, bandwidth of the original signal is B, which is sampled (@ fs) and then quantized for A2D conversion:

-- if sampled at Nyquist rate: fs = 2B
-- if over-sampled, fs = N*2B (where N is the oversampling ratio)

Now, in either of the above 2 cases, the output signal will be bandlimited from -B to +B. But, the quantization noise spectra is from -fs/2 to + fs/2 : depending on the cases above, fs/2 may or may not be = B !



So why is the quantization noise always in that range?

The quantization error produces harmonics which extend well past the nyquist bandwidth of DC to Fs/2. However, all those higher order harmonic must fold back into the nyquist bandwidth and sum together to produce the rms noise. you can think of this process as FIRST doing QUANTIZATION (which produces noise from DC to Higher frequencies than the Nyquist) and then do the SAMPLING which folds the noise to the nyquist band and this is why you will assume that the quantization noise is bandlimited by DC-Fs/2.

jdp721 said:

Please don't mind me elaborating a bit

Say, bandwidth of the original signal is B, which is sampled (@ fs) and then quantized for A2D conversion:

-- if sampled at Nyquist rate: fs = 2B
-- if over-sampled, fs = N*2B (where N is the oversampling ratio)

Now, in either of the above 2 cases, the output signal will be bandlimited from -B to +B. But, the quantization noise spectra is from -fs/2 to + fs/2 : depending on the cases above, fs/2 may or may not be = B !

View attachment 107455

So why is the quantization noise always in that range?

Click to expand...

First, you have indicated in-band noise in your diagram. I assume you don't mean thermal noise or some analog noise source to the input of the A/D. OF course, quantization noise is not thermal noise or analog noise at the input of the A/D. It is modeled as input noise - usually white spectrum (uncorrelated samples) with uniform PDF distribution which is true under certain conditions. I'm not totally sure if your question is "why doesn't the quantization noise land outside the range from -fs/2 to fs/2", or if your question is,"why is it spectrally flat within that range from -fs/2 to fs/2.

That white spectrum means it's flat, evenly distributed from -fs/2 to fs/2. To say that it should be distributed outside that range is to misunderstand frequency aliasing. The normalized digital frequency is θ=wTs. So the nyquist zone from -fs/2 < f < fs/2 corresponds to -pi < θ < pi. So a normalized digital frequency at pi/2 gives

cos(pi/2 n) = [ 1 0 -1 0 1 0 -1 .... ]

Notice that cos(-3pi/2 n) and cos(5pi/2 n) give the same result (because n is an integer - discrete). They are the same discrete time signals, indistinguishable aliases. Any digital frequency θ=pi/2+k*2pi, where k is an integer is an alias of pi/2. In un-normalized frequency domain, any frequency f+kfs is an alias of f.

So why would quantization noise fall in that range from -fs/2 to fs/2? The discrete time spectrum is aliased or repeated every k*fs Hz. The discrete time spectrum from -fs/2 to fs/2 IS the discrete time spectrum from fs/2 to 3fs/2 which IS the discrete time spectrum from 3fs/2 to 5fs/2..

The assumption that it's white noise inside that range is a little more complicated to pin down. But generally, it will not be spectrally flat if the input signal is constant, or periodic, or correlated to the sampling frequency, or.... Take for example, if the input signal is a constant DC. Then the quantized digital code will always be the same, the quantization error will also always be the same, and all of the quantization noise will be DC.