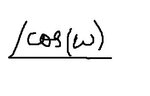SanjKrish
Member level 3

- Joined
- Feb 6, 2011
- Messages
- 67
- Helped
- 1
- Reputation
- 2
- Reaction score
- 1
- Trophy points
- 1,288
- Location
- India
- Activity points
- 1,855
This is a little tricky.. and I tried my best to explain my question..
I was watching a video in DSP posted by NPTEL in IIT video lectures..
He was explaining that....
A simple digital band stop filter's transfer function is given by
X(Z) = 1/2 (1+Z-2)
Replacing Z by ej\[\omega\] and reducing the expression we finally get the frequency response as
H(ej\[\omega\]) = (1/2)e-j\[\omega\] * 2\[\cos\]\[\omega\]
Now the author graphed a plot of cos(\[\omega\]) Vs \[\omega\] first as shown below

He said that cos(\[\omega\]) has 0 phase till \[\pi\]/2 and after \[\pi\]/2 the phase abruptly changes by \[\pi\]
He then came up with an equation for the phase angle, for the above mentioned frequency response equation, as
phase angle = -\[\omega\] + "angle of cos(\[\omega\])"
Now how did he get the phase angle like that.. I really don't understand the "angle of cos(\[\omega\])" part
what does that mean
He then plotted the phase plot of the digital filter like this
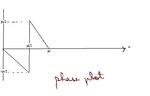
Please explain me how did he arrive at such a phase plot..
why does the the phase plot suddenly jump from -\[\pi\]/2 to +\[\pi\]/2
I was watching a video in DSP posted by NPTEL in IIT video lectures..
He was explaining that....
A simple digital band stop filter's transfer function is given by
X(Z) = 1/2 (1+Z-2)
Replacing Z by ej\[\omega\] and reducing the expression we finally get the frequency response as
H(ej\[\omega\]) = (1/2)e-j\[\omega\] * 2\[\cos\]\[\omega\]
Now the author graphed a plot of cos(\[\omega\]) Vs \[\omega\] first as shown below

He said that cos(\[\omega\]) has 0 phase till \[\pi\]/2 and after \[\pi\]/2 the phase abruptly changes by \[\pi\]
He then came up with an equation for the phase angle, for the above mentioned frequency response equation, as
phase angle = -\[\omega\] + "angle of cos(\[\omega\])"
Now how did he get the phase angle like that.. I really don't understand the "angle of cos(\[\omega\])" part
what does that mean
He then plotted the phase plot of the digital filter like this

Please explain me how did he arrive at such a phase plot..
why does the the phase plot suddenly jump from -\[\pi\]/2 to +\[\pi\]/2
Last edited: