Junus2012
Advanced Member level 5

Dear friends
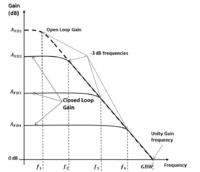
Kindly, why the bandwidth of the unity gain op-amp buffer is defined at the unity gain frequency, while the bandwidth at any different gain is at -3db.
if I apply this principle on the buffer op-amp, then the bandwidth is 0 dB-3 dB = - 3 dB not at 0 dB as from GBW
thank you
Kindly, why the bandwidth of the unity gain op-amp buffer is defined at the unity gain frequency, while the bandwidth at any different gain is at -3db.
if I apply this principle on the buffer op-amp, then the bandwidth is 0 dB-3 dB = - 3 dB not at 0 dB as from GBW
thank you