iVenky
Advanced Member level 2

- Joined
- Jul 11, 2011
- Messages
- 584
- Helped
- 37
- Reputation
- 76
- Reaction score
- 35
- Trophy points
- 1,318
- Location
- College Station, Texas
- Activity points
- 6,124
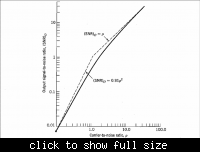
In AM receiver I read that if the SNR is very less then product modulator is better compared to envelope dectector. Why is that so?
Thanks a lot.
Thanks a lot.