Non inverting operational amplifier

Hi!

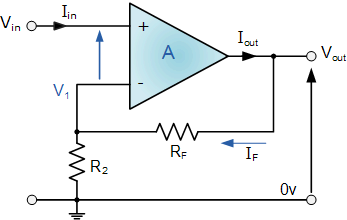
Considering this circuit:

**broken link removed**

Vout = A(Vin -Vout*R2/(R2+Rf)), which simplifies to Vout = Vin*(R2+Rf)/R2.

If we now assume that R2 = Rf, then the gain A = 2. And assume that Vin = 5V.

Then:
1) Initially Vout = 0.
2) After some time Vout = 2*(5-0/2) = 10V
3) After the same time Vout = 2*(5-10/2) = 0V
4) After the same time Vout = 2*(5-0/2) = 10V
5) and so on..

By "some time" I mean the time it takes the Vout*R2/(R2+Rf) appear across V-.

Does this mean the output is jumping from 0 to 10V in very tiny fractions of time? Assuming that the output can't change instantaneously.

Please correct me, if I am wrong, cause this is a very important concept.

Thank you!

Hi NonBio,

the figure is lost (at least I cannot see it), and from your description I'm not sure which is the configuration.
Please, could you upload again the circuit? Thanks.
Regards

Z

Hi NonBio,

Yes, you are wrong: The symbol A stands for the open-loop gain of the opamp (1E4...1E5) - not for the closed-loop gain G=2.
More than that, you must not assume that from the beginning (t=0) the circuit assumes its closed-loop gain.
Consider the feedback action that needs some time.

Thanks for the reply.

But shouldn't it then be Vout = A(V+ - V-) = A(Vin - Vout*R2/(R2+Rf)) = Vin*(R2+Rf)/R2.

If R2 = Rf and Vin = 5V, then Vout = 5*2 = 10V.

Now V+ = Vin = 5V, but V- = 10/2 = 5V,

so Vout = A(5 - 5) = 0? But it's not 0. Why? I just know that, when V+ - V- = 0, the output stays at 10V,

but when V+ - V- < 0, the is pulled down to 10V, and when V+ - V- > 0, the output is pulled up to 10V.

I would be grateful if someone could explain me why that happens.

And the circuit is this, if anyone can't see it. (I can see it in my first post.)

NonBio said:

But shouldn't it then be Vout = A(V+ - V-) = A(Vin - Vout*R2/(R2+Rf)) = Vin*(R2+Rf)/R2.
If R2 = Rf and Vin = 5V, then Vout = 5*2 = 10V.
Now V+ = Vin = 5V, but V- = 10/2 = 5V,
so Vout = A(5 - 5) = 0? But it's not 0. Why?

Click to expand...

Your calcuation is correct because you have assumed (first line) that A is approaching infinity. That's consistent.
In reality it is not 0 because the opamp is a real device.

NonBio said:

I just know that, when V+ - V- = 0, the output stays at 10V,
f[/img]

Click to expand...

How do you know? It's not correct.

NonBio said:

but when V+ - V- < 0, the is pulled down to 10V, and when V+ - V- > 0, the output is pulled up to 10V.
I would be grateful if someone could explain me why that happens.
And the circuit is this, if anyone can't see it. (I can see it in my first post.)

Click to expand...

If you want to understand how an opamp with feedback comes to the steady state (fixed closed-loop gain) you must not assume in your calculation a closed-loop gain G=2 (as I have mentioned already in my first answer) from the very first beginning!. You have to take into consideration the time delay within the feedback loop.
To understand how and why a steady state with a stable operating point (enabling G=2) is achieved you should try to understand the principle and the benefits of negative feedback.

NonBio said:

Vout = A(5 - 5) = 0? But it's not 0. Why?

Click to expand...

You assumed A=Infinity and this assumption gave V-=V+.
So, A*(5-5) is not 0, but an indetermination of the type 0*Inf .

Please take the equation of yout first post:

Vout = A(Vin -Vout*R2/(R2+Rf))

an solve for Vout. You see that only for A->Infinity it simplifies to Vout = Vin*(R2+Rf)/R2.
For finite A, there is no indetermination.
Regards

Z

Am I true to say that:

the new Vout(new) = A*Vin - A*Vout(previous)*R2/(Rf+R2) ?

i.e. Vout(ith) = A*Vin - A*Vout(ith-1)*R2/(Rf+R2) ?

Cause this doesn't work, it results in oscillations from -Inf to +Inf instead (i.e. +12V and -12V in practice, if supply is +-12V).

So this isn't true either. Therefore, the present value of Vout is dependent on the present value of Vout ? I'm confused about this part.

Vout(ith) = A*Vin - A*Vout(ith)*R2/(Rf+R2) ? It's easy, if we rearrange just to get Vout(ith) = A*Vin / (1 + A*R2/(R2+Rf)), but this rearrangement is only valid if Vout taking part at the V- input port is the same as Vout at the output port, but obviously Vout can't appear on V- instantaneously, because it has to travel through the wiring and the Rf resistor, right?

So I am mainly confused about the part of Vout being dependent on Vout.

Or is it just that the voltage Vout travels from Output to V- much, much faster than the op-amp processes it's input and produces the output?

Thanks everyone!

Hi NonBio,

What you are making thinking in that way is equivalent to consider a discrete-time system, or to insert a pure delay at the output of the amplifier.
In reality, we are in continuous time and the response of the amplifier has some rise time (it is not instantaneous). Between what you call "previous" and "new" (or "ith-1" and "ith" instants), the output changes continuously and (if some stability conditions exist) the equilibrium poit is reached after a transient during which the output changes continuously and more or less gracefully.
If you do have a delay and the response of the amplifier is instantaneous (no rise time, or rise time much lower than the delay), then what you said takes place and the system is unstable.

Regards

Z

zorro said:

Hi NonBio,

What you are making thinking in that way is equivalent to consider a discrete-time system, or to insert a pure delay at the output of the amplifier.
In reality, we are in continuous time and the response of the amplifier has some rise time (it is not instantaneous). Between what you call "previous" and "new" (or "ith-1" and "ith" instants), the output changes continuously and (if some stability conditions exist) the equilibrium poit is reached after a transient during which the output changes continuously and more or less gracefully.
If you do have a delay and the response of the amplifier is instantaneous (no rise time, or rise time much lower than the delay), then what you said takes place and the system is unstable.

Regards

Z

Click to expand...

So the output of the op-amp doesn't go to, say, +12 V instantaneously, but takes some time, which is larger than the time taken for the output voltage to appear on the V- input?

Therefore, voltage at V- input rises as fast as the voltage at Vout output. The Vout keeps rising, until V- gets > 5V, then it starts decreasing, until V- gets < 5V, and it does this all the time, providing a stable output voltage Vout.

And because of this continuous motion, when V- hits 5V, the output can't suddenly drop to 0V, but it is tending to do so, therefore, V- gets below 5V, say 4.9999, the Vout is expected to go 1V, therefore it decreases slower, until the output is expected to be higher than it is, then it increases, and so on.

So the method is: as the output increases, the difference at the input decreases and, as the output decreases, the difference at the input increases, providing a constant voltage?

Did I finally get it right?

And for a circuit with Rf = R2, A = 10000, Vin = 5V, Supply = +-12V, I would get Vout varying between 9.9976 and 10.0024V, producing 10V on average.

And for a circuit with Rf = R2, A = 10000, Vin = 5V, Supply = +-12V, I would get Vout varying between 9.9976 and 10.0024V, producing 10V on average.

Click to expand...

The variation numbers suggest that you did a calculation with open loop gain. It's basically wrong.

You won't expect any variation as long there are no external disturbances causing it, independent of the amplifier open loop gain A. In connection with zorro's visual explanation: The nature of the time continuous, linear system results in a stable steady state for all involved circuit nodes. Only electronic noise is causing some very small fluctuations.

FvM said:

The variation numbers suggest that you did a calculation with open loop gain. It's basically wrong.

You won't expect any variation as long there are no external disturbances causing it, independent of the amplifier open loop gain A. In connection with zorro's visual explanation: The nature of the time continuous, linear system results in a stable steady state for all involved circuit nodes. Only electronic noise is causing some very small fluctuations.

Click to expand...

So the output goes from 0 to 10V without any oscillations and then stays at 10V? But there should be a tiny variation of a magnitude of fV or smth?

So the output goes from 0 to 10V without any oscillations and then stays at 10V?

Click to expand...

For simplicity, let us assume that you are talking about the output response to an input step. There may be an overshoot or even a short decaying oscillation, according to amplifier frequency characteristic and also large signal behaviour. That's still very different from the previously assumed permanent output voltage variation. But with respective frequency compensation, the settling can be truely monotonic.

But there should be a tiny variation of a magnitude of fV or smth?

Click to expand...

As already said, there's electronic noise. You can expect nV, uV or more, depending on amplifier and measurent bandwidth. But it's caused by a random process, nothing like an oscillatory variation of output voltage as previously assumed.

Thanks to all of you, who responded!

I finally got the concept of negative feedback. :wink: