student2005
Member level 3

full adder circuit
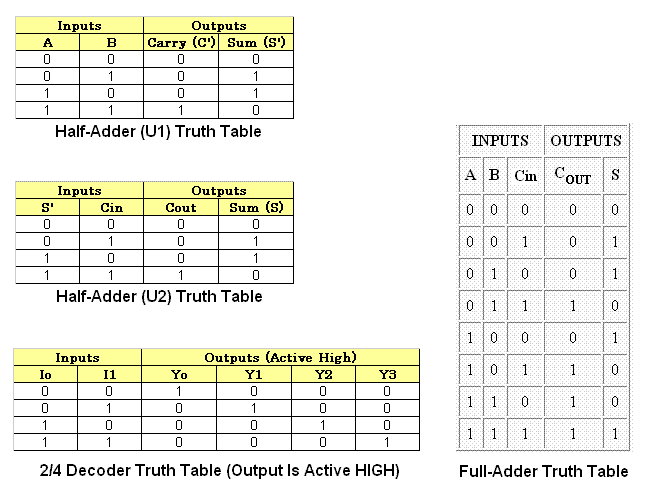
Is it possible to build a FULL ADDER circuit using 2-4 decoder & OR gate? Pls advise the approach if it's possible. Many thanks.
Is it possible to build a FULL ADDER circuit using 2-4 decoder & OR gate? Pls advise the approach if it's possible. Many thanks.