RichardS
Newbie level 4

- Joined
- Jun 1, 2016
- Messages
- 6
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1
- Activity points
- 49
Hi,
I need help with calculating my circuit, I've done something but not sure if that is correct. Any help or direction where to look at is welcome. In the end I need transfer function of the circuit.
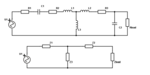
The first circuit is the one I start with, the second picture is "simplified" circuit with impedance for easier calculation.
Where
Z1=(1/Cin*s) + R1 + R2 + L1*s
Z2 = R3+L2*s
Z3 = L3*s
Zload = Rload + (1/C2*s) ?
What I need is
uout/uin =
i1/uin =
i2/uin =
i2/i1 =
where uout is voltage on load and uin is entry voltage u1
View attachment 129484
I need help with calculating my circuit, I've done something but not sure if that is correct. Any help or direction where to look at is welcome. In the end I need transfer function of the circuit.
The first circuit is the one I start with, the second picture is "simplified" circuit with impedance for easier calculation.
Where
Z1=(1/Cin*s) + R1 + R2 + L1*s
Z2 = R3+L2*s
Z3 = L3*s
Zload = Rload + (1/C2*s) ?
What I need is
uout/uin =
i1/uin =
i2/uin =
i2/i1 =
where uout is voltage on load and uin is entry voltage u1
View attachment 129484
Last edited by a moderator: