preethi19
Full Member level 5

- Joined
- Jun 30, 2014
- Messages
- 273
- Helped
- 0
- Reputation
- 0
- Reaction score
- 1
- Trophy points
- 16
- Activity points
- 3,474
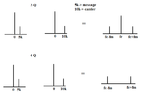
Hi i am able to understand that two quadrant just has one input (bipolar) and another input to be unipolar. While 4 quadrant has both inputs bipolar. And also 2 quad multiplier is an unbalanced modulator while 4-q is balanced meaning 2-Q has carrier and sidebands while 4-Q has carrier supressed.
But can anyone pls explain the difference between both 2-Q and 4-Q multipliers (in terms of AM). In 2-Q one input is ac signal and other is DC. So the wave appears for postive cycle. so does that mean for the positive cycle the carrier is modulated resulting in the sidebands and during the negative cycle no modulation occurs and thus the unmodulated carrier is present at the negative cycle of the O/p. Can anyone pls tell if this is right...
Also in 4-Q what exactly happens that the carrier is suppressed? This is the main thing between those two which i'm not quite sure about. Can anyone pls help!!! Thank you!!!
But can anyone pls explain the difference between both 2-Q and 4-Q multipliers (in terms of AM). In 2-Q one input is ac signal and other is DC. So the wave appears for postive cycle. so does that mean for the positive cycle the carrier is modulated resulting in the sidebands and during the negative cycle no modulation occurs and thus the unmodulated carrier is present at the negative cycle of the O/p. Can anyone pls tell if this is right...
Also in 4-Q what exactly happens that the carrier is suppressed? This is the main thing between those two which i'm not quite sure about. Can anyone pls help!!! Thank you!!!
Last edited: