micro7311
Junior Member level 2

- Joined
- Jun 21, 2015
- Messages
- 22
- Helped
- 0
- Reputation
- 0
- Reaction score
- 0
- Trophy points
- 1
- Activity points
- 199
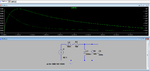
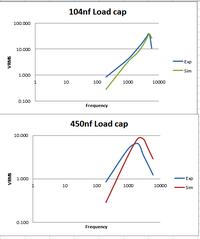
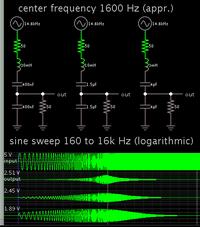
Hi, I have the attached circuit and I am looking for information on what external components can be added to make the plot "fall" faster after the resonant frequency. Keeping all values the same, what other passives (RLC) can be added to make the response drop more rapidly and have a higher Q factor?