palmeiras
Full Member level 6

- Joined
- Feb 22, 2010
- Messages
- 375
- Helped
- 61
- Reputation
- 122
- Reaction score
- 50
- Trophy points
- 1,308
- Location
- South America
- Activity points
- 4,199
Hello guys,
Please, can someone help me with the following doubts about the traditional PTAT circuit?
(a) How does the positive feedback work in this circuit?
(b) How can I simulate the stability of this circuit using HSPICE?
(c) When the circuit presents a positive feedback, how can I ensure a stable operating point? Sedra Microelectronics book says that making K > 1.0 avoid instability. For me it is not clear. I know that making K higher than 1 we have Iout different than zero, but this does not explain the stability issue.
Thank you very much in advance,
Best regards,
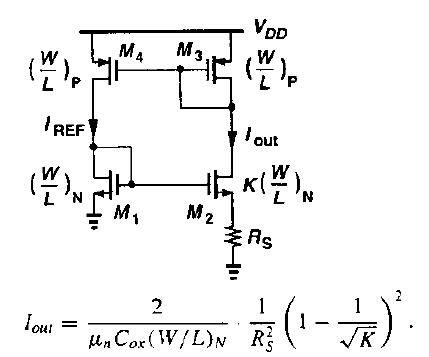
Please, can someone help me with the following doubts about the traditional PTAT circuit?
(a) How does the positive feedback work in this circuit?
(b) How can I simulate the stability of this circuit using HSPICE?
(c) When the circuit presents a positive feedback, how can I ensure a stable operating point? Sedra Microelectronics book says that making K > 1.0 avoid instability. For me it is not clear. I know that making K higher than 1 we have Iout different than zero, but this does not explain the stability issue.
Thank you very much in advance,
Best regards,





