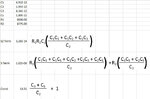Tony614
Newbie level 4

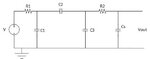
I am trying to determine the time constant for the following circuit:

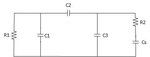
V is a DC voltage source. It is 0V at t<0. At t=0 it goes to voltage V. Cs is a sampling cap. I am interested in the time constant at Vout. I'm a bit unsure whether I can treat this is a DC problem since I'm interested in the charge time which is inherently a non-constant signal. But assuming I can treat this as DC, then I short the DC source and get this:

This is where I get stuck. The C3 branch and the R2-Cs branch have the same voltage across them so they are in parallel. But I don't think I can just combine C3 and Cs since R2 is on the second branch. And even if I could, I sill have an RC on the left and an RC on the right connected by C2. How do I reduce those elements?

V is a DC voltage source. It is 0V at t<0. At t=0 it goes to voltage V. Cs is a sampling cap. I am interested in the time constant at Vout. I'm a bit unsure whether I can treat this is a DC problem since I'm interested in the charge time which is inherently a non-constant signal. But assuming I can treat this as DC, then I short the DC source and get this:

This is where I get stuck. The C3 branch and the R2-Cs branch have the same voltage across them so they are in parallel. But I don't think I can just combine C3 and Cs since R2 is on the second branch. And even if I could, I sill have an RC on the left and an RC on the right connected by C2. How do I reduce those elements?